Question

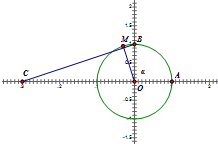如图，A、B是单位圆与x轴、y轴正半轴的交点，点M在单位圆上，∠AOM=α（0＜α＜π），点C（-3，0），若BC⊥OM，则sin（2α-

π

3

）=（　　）

• A、

  4 3 -3

  10

• B、

  2 3 +3

  10

• C、

  4 3 +3

  10

• D、

  2 3 -3

  10

Answer 1

考点：两角和与差的正弦函数

专题：三角函数的求值

分析：由BC坐标，求出直线BC的斜率，进而根据BC⊥OM，可得OM的斜率，即α的正切值，进而利用同角三角函数基本关系式，求出sinα，cosα，进而利用倍角公式和差角公式，可得答案．

解答： 解：由图知B（0，1），C（-3，0），
所以kBC=

1

3

，
而∠AOM=α（0＜α＜π）且BC⊥OM，
从而k_OM=tanα=-3，
则sinα=

3 10

10

，cosα=-

10

10

，
sin2α=-

3

5

，cos2α=-

4

5

，
sin(2α-

π

3

)=(-

3

5

)×

1

2

-(-

4

5

)×

3

2

=

4 3 -3

10

，
故选A；

点评：本题考查的知识点是两角差的正弦公式，倍角公式，同角三角函数关系，难度中档．