题目内容
已知非零向量
,
,
满足:|
+
|=|
-
|,|
|=|
|=|
+
+
|=1,则
的范围是 .
| a |
| b |
| c |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| c |
| ||||
|
|
考点:平面向量数量积的运算
专题:平面向量及应用
分析:由题意可得
⊥
,建立直角坐标系,可得
=(1,0),
=(0,1),设
=(x,y),由条件可得-2≤x≤0,即为所求范围.
| a |
| b |
| a |
| b |
| c |
解答:
解:由|
+
|=|
-
|平方可得
•
=0,可得
⊥
,
又|
|=|
|=|
+
+
|=1,故可建立直角坐标系,
可得
=(1,0),
=(0,1),设
=(x,y),
由|
+
+
|=1可得(x+1)2+(y+1)2=1,
由圆的知识可知-2≤x≤0,
∴
=x∈[-2,0]
故答案为:[-2,0]
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
又|
| a |
| b |
| a |
| b |
| c |
可得
| a |
| b |
| c |
由|
| a |
| b |
| c |
由圆的知识可知-2≤x≤0,
∴
| ||||
|
|
故答案为:[-2,0]
点评:本题考查平面向量的数量积,涉及坐标系的建立和圆的知识,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
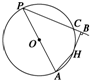 如图所示,PA为⊙O的直径,PC为⊙O的弦,过弧AC的中点H作PC的垂线交PC的延长线于点B.若HB=4,BC=2,则⊙O的直径为( )
如图所示,PA为⊙O的直径,PC为⊙O的弦,过弧AC的中点H作PC的垂线交PC的延长线于点B.若HB=4,BC=2,则⊙O的直径为( )| A、10 | B、13 | C、15 | D、20 |
下列函数是偶函数的是( )
| A、y=lgx2 | ||
B、y=(
| ||
| C、y=1-x2,x∈(-1,1] | ||
| D、y=x-1 |
若k>1,a>0,则k2a2+
取得最小值时,a的值为( )
| 16 |
| (k-1)a2 |
| A、1 | ||
B、
| ||
| C、2 | ||
| D、4 |