题目内容
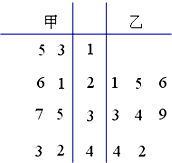 以下茎叶图记录了甲、乙两名篮球运动员在以往几场比赛中得分的情况,设甲、乙两组数据的平均数分别为
以下茎叶图记录了甲、乙两名篮球运动员在以往几场比赛中得分的情况,设甲、乙两组数据的平均数分别为. |
| x甲 |
. |
| x乙 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:茎叶图
专题:概率与统计
分析:根据茎叶图中的数据,求出甲、乙的平均数和方差,得出标准差,通过比较可以得出结论.
解答:
解:根据茎叶图中的数据,得;
甲的平均数是
=
(13+15+21+26+35+37+42+43)=29,
乙的平均数是
=
(21+25+26+33+34+39+44+42)=33;
甲的方差是s甲2=
[(13-29)2+(15-29)2+(21-29)2+(26-29)2+(35-29)2+(37-29)2+(42-29)2+(43-29)2]=
,
标准差是s甲=
;
乙的方差是s乙2=
[(21-33)2+(25-33)2+(26-33)2+(33-33)2+(34-33)2+(39-33)2+(44-33)2+(42-33)2]=
,
标准差是s乙=
;
∴
<
,s甲>s乙.
故选:B.
甲的平均数是
. |
| x甲 |
| 1 |
| 8 |
乙的平均数是
. |
| x乙 |
| 1 |
| 8 |
甲的方差是s甲2=
| 1 |
| 8 |
| 495 |
| 4 |
标准差是s甲=
|
乙的方差是s乙2=
| 1 |
| 8 |
| 248 |
| 4 |
标准差是s乙=
|
∴
. |
| x甲 |
. |
| x乙 |
故选:B.
点评:本题考查了利用茎叶图中的数据求平均数和方差的问题,作为选择题也可以利用平均数与方差表示的含义,估算出结果,是基础题.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
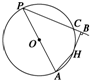 如图所示,PA为⊙O的直径,PC为⊙O的弦,过弧AC的中点H作PC的垂线交PC的延长线于点B.若HB=4,BC=2,则⊙O的直径为( )
如图所示,PA为⊙O的直径,PC为⊙O的弦,过弧AC的中点H作PC的垂线交PC的延长线于点B.若HB=4,BC=2,则⊙O的直径为( )| A、10 | B、13 | C、15 | D、20 |
下列函数是偶函数的是( )
| A、y=lgx2 | ||
B、y=(
| ||
| C、y=1-x2,x∈(-1,1] | ||
| D、y=x-1 |
若直线(2a+b)x+y-1=0(a>0,b>0)经过椭圆
+
=1的右焦点,则
+
的最小值是( )
| x2 |
| 4 |
| y2 |
| 3 |
| 1 |
| a |
| 1 |
| b |
A、
| ||
| B、4 | ||
C、3+2
| ||
| D、6 |
设{an}是等比数列,若a2=3,a7=1,则数列{an}前8项的积为( )
| A、56 | B、80 | C、81 | D、128 |
下列函数是偶函数,且在(0,+∞)上单调递增的是( )
| A、y=x3 |
| B、y=lgx |
| C、y=|x| |
| D、y=1-x2 |
若k>1,a>0,则k2a2+
取得最小值时,a的值为( )
| 16 |
| (k-1)a2 |
| A、1 | ||
B、
| ||
| C、2 | ||
| D、4 |
已知{an}为等比数列,a5+a8=2,a6•a7=-8,则a2+a11=( )
| A、5 | B、7 | C、-7 | D、-5 |