题目内容
下列求导运算正确的是（ ）
| A、（sinx）′=-cosx | ||||
| B、（cosx）′=sinx | ||||
C、（
| ||||
| D、（2x）′=x•2x-1 |
考点：导数的运算
专题：导数的概念及应用
分析：根据常见函数的导数公式即可得到结论．
解答：
解：（sinx）′=cosx，故A错误．
（cosx）′=-sinx，故B错误．
（
）′=-
，故C正确．
（2x）′=ln2•2x，故D错误，
故选：C．
（cosx）′=-sinx，故B错误．
（
| 1 |
| x |
| 1 |
| x2 |
（2x）′=ln2•2x，故D错误，
故选：C．
点评：本题主要考查导数的计算，要求熟练掌握常见函数的导数公式．
练习册系列答案
相关题目
圆的方程是
（θ为参数），则这个圆的半径是（ ）
|
| A、1 | ||
| B、2 | ||
C、
| ||
D、
|
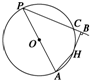如图所示，PA为⊙O的直径，PC为⊙O的弦，过弧AC的中点H作PC的垂线交PC的延长线于点B．若HB=4，BC=2，则⊙O的直径为（ ）| A、10 | B、13 | C、15 | D、20 |
已知数列{an}满足条件：a1=
，an+1=
(n∈N+)，则对n≤20的正整数，an+an+1=
的概率为（ ）
| 1 |
| 2 |
| 1+an |
| 1-an |
| 1 |
| 6 |
A、
| ||
B、
| ||
C、
| ||
| D、0 |
若直线（2a+b）x+y-1=0（a＞0，b＞0）经过椭圆
+
=1的右焦点，则
+
的最小值是（ ）
| x2 |
| 4 |
| y2 |
| 3 |
| 1 |
| a |
| 1 |
| b |
A、
| ||
| B、4 | ||
C、3+2
| ||
| D、6 |
定义在R上的可导函数f（x），当x∈（1，+∞）时，（x-1）f′（x）-f（x）＞0恒成立，a=f（2），b=
f（3），c=（
+1）f（
），则a、b、c的大小关系为（ ）
| 1 |
| 2 |
| 2 |
| 2 |
| A、c＜a＜b |
| B、b＜c＜a |
| C、a＜c＜b |
| D、c＜b＜a |