题目内容
设f(x)定义域为(-2,2),则f(
)+f(
)的定义域为 .
| x |
| 2 |
| 2 |
| x |
考点:函数的定义域及其求法
专题:函数的性质及应用
分析:根据复合函数定义域之间的关系即可得到结论.
解答:
解:∵f(x)定义域为(-2,2),
∴要使函数有意义,则
,
即
,
则1<x<4或-4<x<-1,
即函数定义域为{x|1<x<4或-4<x<-1},
故答案为:{x|1<x<4或-4<x<-1}
∴要使函数有意义,则
|
即
|
则1<x<4或-4<x<-1,
即函数定义域为{x|1<x<4或-4<x<-1},
故答案为:{x|1<x<4或-4<x<-1}
点评:本题主要考查函数定义域的求解,根据复合函数定义域之间的关系是解决本题的关键.

练习册系列答案
相关题目
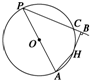 如图所示,PA为⊙O的直径,PC为⊙O的弦,过弧AC的中点H作PC的垂线交PC的延长线于点B.若HB=4,BC=2,则⊙O的直径为( )
如图所示,PA为⊙O的直径,PC为⊙O的弦,过弧AC的中点H作PC的垂线交PC的延长线于点B.若HB=4,BC=2,则⊙O的直径为( )| A、10 | B、13 | C、15 | D、20 |
下列函数是偶函数,且在(0,+∞)上单调递增的是( )
| A、y=x3 |
| B、y=lgx |
| C、y=|x| |
| D、y=1-x2 |
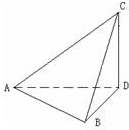 如图,将边长为1m的正△ABC沿高AD折叠成直二面角B-AD-C,则直线AC与直线AB所成角的余弦值是
如图,将边长为1m的正△ABC沿高AD折叠成直二面角B-AD-C,则直线AC与直线AB所成角的余弦值是