题目内容
 已知圆O:x2+y2=4.
已知圆O:x2+y2=4.(1)直线l1:
| 3 |
| 3 |
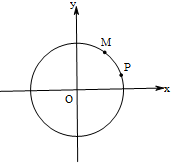
(2)如图,设M(x1,y1)、P(x2,y2)是圆O上的两个动点,点M关于原点的对称点为M1,点M关于x轴的对称点为M2,如果直线PM1、PM2与y轴分别交于(0,m)和(0,n),问m•n是否为定值?若是求出该定值;若不是,请说明理由;
(3)过O点任作一直线与直线x=4交于E点,过(2,0)点作直线与OE垂直,并且交直线x=4于F点,以EF为直径的圆是否过定点,如过定点求出其坐标,如不过,请说明理由.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)先求出圆心(0,0)到直线:
x+y-2
=0的距离,再利用弦长公式求得弦长AB的值.
(2)先求出M1和点M2的坐标,用两点式求直线PM1 和PM2的方程,根据方程求得他们在y轴上的截距m、n的值,计算mn的值,可得结论.
(3)设直线OE的方程为y=kx,且E(4,4k),设与OE垂直的直线l: y=-
(x-2),由此利用已知条件能推导出以EF为直径的圆过定点(4±2
,0).
| 3 |
| 3 |
(2)先求出M1和点M2的坐标,用两点式求直线PM1 和PM2的方程,根据方程求得他们在y轴上的截距m、n的值,计算mn的值,可得结论.
(3)设直线OE的方程为y=kx,且E(4,4k),设与OE垂直的直线l: y=-
| 1 |
| k |
| 2 |
解答:
解:(1)∵圆O:x2+y2=4圆心的圆心O(0,0),半径r=2,
圆心O(0,0)到直线l1:
x+y-2
=0的距离d=
=
.
∴|AB|=2
=2.…4分
(2)∵M(x1,y1)、p(x2,y2)是圆O上的两个动点,
∴M1(-x1,-y1),N(x1,-y1),且x12+y12=4,x22+y22=4,…(6分)
根据PM1的方程为
=
,令x=0,得y=m=
.
根据PM2的方程为:
=
,令x=0,得y=n=
.…(8分)
∴m•n=
=
=4,
∴m•n为定值4.…(10分)
(3)解:设直线OE的方程为y=kx,且E(4,4k)
设与OE垂直的直线为l∴l: y=-
(x-2)
令x=4, y=-
∴F(4,-
)…(12分)
设M(x0,y0)为圆上一点,以EF为直径,
∴
•
=0,∴(4-x0)2+(4k-y0)•(-
-y0)=0…(14分)
由对称性可知,定点必在x轴上,∴y0=0,
即(4-x0)2-4k•
=0,∴x0=4±2
,
∴以EF为直径的圆过定点(4±2
,0).…(16分)
圆心O(0,0)到直线l1:
| 3 |
| 3 |
|0+0-2
| ||
|
| 3 |
∴|AB|=2
22-(
|
(2)∵M(x1,y1)、p(x2,y2)是圆O上的两个动点,
∴M1(-x1,-y1),N(x1,-y1),且x12+y12=4,x22+y22=4,…(6分)
根据PM1的方程为
| y+y1 |
| y2+y1 |
| x+x1 |
| x2+x1 |
| x1y2-x2y1 |
| x2+x1 |
根据PM2的方程为:
| y+y1 |
| y2+y1 |
| x-x1 |
| x2-x1 |
| -x1y2-x2y1 |
| x2-x1 |
∴m•n=
| x22y12-x12y22 |
| x22-x12 |
| x22(4-x12)-x12(4-x22) |
| x12-x22 |
∴m•n为定值4.…(10分)
(3)解:设直线OE的方程为y=kx,且E(4,4k)
设与OE垂直的直线为l∴l: y=-
| 1 |
| k |
令x=4, y=-
| 2 |
| k |
| 2 |
| k |
设M(x0,y0)为圆上一点,以EF为直径,
∴
| ME |
| MF |
| 2 |
| k |
由对称性可知,定点必在x轴上,∴y0=0,
即(4-x0)2-4k•
| 2 |
| k |
| 2 |
∴以EF为直径的圆过定点(4±2
| 2 |
点评:本题主要考查直线和圆相交的性质,点到直线的距离公式,用两点式求直线的方程、求直线在y轴上的截距,考查圆是否过定点的判断及定点坐标的求法.

练习册系列答案
相关题目
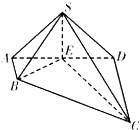 如图,四棱锥S-ABCD中,AB⊥AD,AB∥CD,CD=3AB=3,平面SAD⊥平面ABCD,E是线段AD上一点,AE=ED=
如图,四棱锥S-ABCD中,AB⊥AD,AB∥CD,CD=3AB=3,平面SAD⊥平面ABCD,E是线段AD上一点,AE=ED= 如图,四棱锥P-ABCD中,底面ABCD是边长为2的正方形,PB⊥BC,PD⊥CD,且PA=2,E为PD中点.
如图,四棱锥P-ABCD中,底面ABCD是边长为2的正方形,PB⊥BC,PD⊥CD,且PA=2,E为PD中点.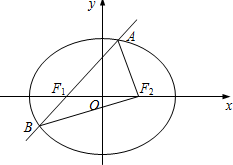 如图,椭圆E:
如图,椭圆E: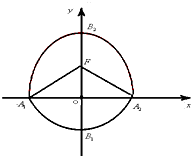 如图,曲线C由半椭圆
如图,曲线C由半椭圆