题目内容
曲线C上的动点P是坐标为(
cosθ,
sinθ).
(1)求曲线C的普通方程,并指出曲线的类型及焦点坐标;
(2)过点Q(2,1)作曲线C的两条切线l1、l2,证明l1⊥l2.
| 3 |
| 2 |
(1)求曲线C的普通方程,并指出曲线的类型及焦点坐标;
(2)过点Q(2,1)作曲线C的两条切线l1、l2,证明l1⊥l2.
考点:直线与圆锥曲线的关系,椭圆的标准方程
专题:圆锥曲线的定义、性质与方程
分析:(1)设出P的直角坐标,消去θ即可得到曲线C的普通方程,并指出曲线的类型及焦点坐标;
(2)设出过点Q(2,1)作曲线C的切线方程,联立直线与椭圆方程,利用判别式为0,即可证明l1⊥l2.
(2)设出过点Q(2,1)作曲线C的切线方程,联立直线与椭圆方程,利用判别式为0,即可证明l1⊥l2.
解答:
解:(1)设P(x,y),由题意
,消去θ,
可得:
+
=1------(2分)
焦点在x轴的椭圆------(4分)
焦点坐标为(±1,0)------(6分)
(2)易知过Q的直线斜率不存在时与曲线C无交点,不相切;------(7分)
设过Q的直线l:y=k(x-2)+1
由
得(2+3k2)x2-6k(2k-1)x+3(2k-1)2-6=0
若l与曲线C相切则△=36k2(2k-1)2-12(2+3k2)((2k-1)2-2)=0
得k2-4k-1=0,则l1,l2的斜率为方程的两根
有k1•k2=-1------(11分)
∴l1⊥l2------(12分)
|
可得:
| x2 |
| 3 |
| y2 |
| 2 |
焦点在x轴的椭圆------(4分)
焦点坐标为(±1,0)------(6分)
(2)易知过Q的直线斜率不存在时与曲线C无交点,不相切;------(7分)
设过Q的直线l:y=k(x-2)+1
由
|
若l与曲线C相切则△=36k2(2k-1)2-12(2+3k2)((2k-1)2-2)=0
得k2-4k-1=0,则l1,l2的斜率为方程的两根
有k1•k2=-1------(11分)
∴l1⊥l2------(12分)
点评:本题考查直线与椭圆的位置关系,参数方程与直角坐标方程的互化,考查转化思想以及计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设M是椭圆
+
=1上的一点,F1、F2为焦点,∠F1MF2=
,则S△ MF1F2为( )
| x2 |
| 25 |
| y2 |
| 16 |
| π |
| 3 |
A、
| ||||
B、16
| ||||
C、
| ||||
D、25
|
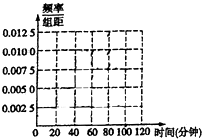 某中学为研究学生的身体素质与课外体育锻炼时间的关系,对400名高一学生的一周课外体育锻炼时间进行调查,结果如下表所示:
某中学为研究学生的身体素质与课外体育锻炼时间的关系,对400名高一学生的一周课外体育锻炼时间进行调查,结果如下表所示: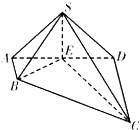 如图,四棱锥S-ABCD中,AB⊥AD,AB∥CD,CD=3AB=3,平面SAD⊥平面ABCD,E是线段AD上一点,AE=ED=
如图,四棱锥S-ABCD中,AB⊥AD,AB∥CD,CD=3AB=3,平面SAD⊥平面ABCD,E是线段AD上一点,AE=ED= 如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC.
如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC. 如图,四棱锥P-ABCD中,底面ABCD是边长为2的正方形,PB⊥BC,PD⊥CD,且PA=2,E为PD中点.
如图,四棱锥P-ABCD中,底面ABCD是边长为2的正方形,PB⊥BC,PD⊥CD,且PA=2,E为PD中点.