Question

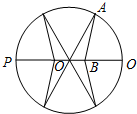为迎接省运会在我市召开，美化城市，在某主干道上布置系列大型花盆，该圆形花盆直径2米，内部划分为不同区域种植不同花草．如图所示，在蝶形区域内种植百日红，该蝶形区域由四个对称的全等三角形组成，其中一个三角形OAB的顶点O为圆心，A在圆周上，B在半径OQ上，设计要求∠ABO=120°．
（1）请设置一个变量x，写出该蝶形区域的面积S关于x的函数表达式；
（2）x为多少时，该蝶形区域面积S最大？

Answer 1

考点：正弦定理

专题：解三角形

分析：（1）设∠AOB=x，在三角形AOB中，由正弦定理表示出OB，S为4个三角形AOB面积，表示出S与x关系式即可；
（2）由（1）的结论整理S，利用正弦函数的值域确定出S最大时x的值即可．

解答： 解：（1）设∠AOB=x，在三角形AOB中，由正弦定理得

AB

sinx

=

OB

sin(60°-x)

=

OA

sin120°

=

1

3 2

，
∴OB=

2

3

sin（60°-x），
则S=4S_△AOB=2OA•OBsinx=

4

3

sin（60°-x）sinx；
（2）由（1）整理得：S=

4

3

（

3

2

cosx+

1

2

sinx）sinx=

2 3

3

sin（2x+30°）-

3

3

，
则x=30°时，蝶形区域面积最大．

点评：此题考查了正弦定理，两角和与差的正弦函数公式，以及三角形面积公式，熟练掌握正弦定理是解本题的关键．