题目内容
已知函数f(x)=Asinwx+Bcoswx(其中A、B、w是常数w>0)的最小周期为2,并且当x=
取得最大值2.
(1)求函数f(x)的表达式
(2)在闭区间[
,
]上是否存在f(x)对称轴,如果存在,求出其对称轴方程;如果不存在,说明理由.
| 1 |
| 3 |
(1)求函数f(x)的表达式
(2)在闭区间[
| 21 |
| 4 |
| 23 |
| 4 |
考点:由y=Asin(ωx+φ)的部分图象确定其解析式,两角和与差的正弦函数,正弦函数的对称性
专题:三角函数的图像与性质
分析:(1)利用辅助角公式可知f(x)=2sin(πx+θ),又f(
)=2sin(
+θ)=2,|θ|<
,可求得θ=
,于是可得函数f(x)的表达式;
(2)
≤x≤
⇒4π+
≤πx+
≤4π+
(k∈Z),利用正弦函数的单调性质可知,当πx+
=4π+
时,f(x)有最小值-2,解得x=
,于是可得答案.
| 1 |
| 3 |
| π |
| 3 |
| π |
| 2 |
| π |
| 6 |
(2)
| 21 |
| 4 |
| 23 |
| 4 |
| 17π |
| 12 |
| π |
| 6 |
| 23π |
| 12 |
| π |
| 6 |
| 3π |
| 2 |
| 16 |
| 3 |
解答:
解:(1)f(x)=
sin(wx+θ)(其中θ为辅助角|θ|<
)
由题意得
=2,
=2,∴w=π;
∴f(x)=2sin(πx+θ),又f(
)=2sin(
+θ)=2,|θ|<
,
∴θ=
,∴f(x)=2sin(πx+
),(6分)
(2)∵
≤x≤
,∴
≤πx+
≤
,即4π+
≤πx+
≤4π+
(k∈Z),
当πx+
=4π+
时,f(x)有最小值-2,解得x=
;
∴在闭区间[
,
]上存在f(x)的对称轴,其方程为x=
.
| A2+B2 |
| π |
| 2 |
由题意得
| A2+B2 |
| 2π |
| w |
∴f(x)=2sin(πx+θ),又f(
| 1 |
| 3 |
| π |
| 3 |
| π |
| 2 |
∴θ=
| π |
| 6 |
| π |
| 6 |
(2)∵
| 21 |
| 4 |
| 23 |
| 4 |
| 65π |
| 12 |
| π |
| 6 |
| 71π |
| 12 |
| 17π |
| 12 |
| π |
| 6 |
| 23π |
| 12 |
当πx+
| π |
| 6 |
| 3π |
| 2 |
| 16 |
| 3 |
∴在闭区间[
| 21 |
| 4 |
| 23 |
| 4 |
| 16 |
| 3 |
点评:本题考查两角和与差的正弦函数,考查辅助角公式的应用,突出考查正弦函数的单调性与对称轴,属于中档题.

练习册系列答案
相关题目
抛物线y2=12x的焦点为( )
| A、(6,0) |
| B、(0,6) |
| C、(3,0) |
| D、(0,3) |
直线x+
y-3=0的倾斜角为( )
| 3 |
| A、30° | B、60° |
| C、120° | D、150° |
已知函数f(x)=asinx+bx3+4(a∈R,b∈R),f′(x)为f(x)的导函数,则f(2014)+f(-2014)+f′(2015)-f′(-2015)=( )
| A、0 | B、2014 |
| C、2015 | D、8 |
在空间直角坐标系中,已知两点A(1,-3,4),B(-3,2,0),则线段AB的中点坐标为( )
A、(-1,-
| ||
| B、(-2,-1,4) | ||
C、(2,-
| ||
| D、(-2,-3,2) |

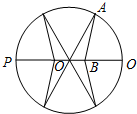 为迎接省运会在我市召开,美化城市,在某主干道上布置系列大型花盆,该圆形花盆直径2米,内部划分为不同区域种植不同花草.如图所示,在蝶形区域内种植百日红,该蝶形区域由四个对称的全等三角形组成,其中一个三角形OAB的顶点O为圆心,A在圆周上,B在半径OQ上,设计要求∠ABO=120°.
为迎接省运会在我市召开,美化城市,在某主干道上布置系列大型花盆,该圆形花盆直径2米,内部划分为不同区域种植不同花草.如图所示,在蝶形区域内种植百日红,该蝶形区域由四个对称的全等三角形组成,其中一个三角形OAB的顶点O为圆心,A在圆周上,B在半径OQ上,设计要求∠ABO=120°.