题目内容
乙两艘轮船都要停靠同一个泊位，它们可以在一昼夜（零点至24点）的任意时刻到达，设甲、乙两艘轮船停靠泊位的时间分别是3小时和5小时，则有一艘轮船停靠泊位时必须等待一段时间的概率．
考点：几何概型
专题：概率与统计
分析：由题意可知如两船到达的时间间隔超过了停泊的时间则不需要等待，要求一艘船停靠泊位时必须等待一段时间的概率即计算一船到达的时间恰好另一船还没有离开，此即是所研究的事件．
解答：
解：设甲船在x点到达，乙船在y点到达，必须等待的事件需要满足如下条件
P（A）=
=
故答案为：
|
P（A）=
24×24-
| ||||
| 24×24 |
| 175 |
| 576 |
故答案为：
| 175 |
| 576 |
点评：考查几何概率模型，考查用图形法求概率，求解此类题的关键是得出所给的事件对应的约束条件，作出符合条件的图象，由图形的测度得出相应的概率．
练习册系列答案
相关题目
已知函数f（x）=asinx+bx3+4（a∈R，b∈R），f′（x）为f（x）的导函数，则f（2014）+f（-2014）+f′（2015）-f′（-2015）=（ ）
| A、0 | B、2014 |
| C、2015 | D、8 |
已知函数f（x）=
，则f（-4）的值是（ ）
|
| A、-2 | B、-1 | C、0 | D、1 |
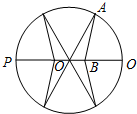为迎接省运会在我市召开，美化城市，在某主干道上布置系列大型花盆，该圆形花盆直径2米，内部划分为不同区域种植不同花草．如图所示，在蝶形区域内种植百日红，该蝶形区域由四个对称的全等三角形组成，其中一个三角形OAB的顶点O为圆心，A在圆周上，B在半径OQ上，设计要求∠ABO=120°．