题目内容
已知抛物线y2=2px,过其焦点F的直线交抛物线于A.B两点,设A.B在抛物线的准线上的射影分别是A1.B1,则∠A1FB1=( )
| A、45° | B、60° |
| C、90° | D、120° |
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:由抛物线的定义及内错角相等,可得∠AFA1=∠A1FK,同理可证∠BFB1=∠B1FK,再利用平角为180°,即∠AFA1+∠A1FK+∠BFB1+∠B1FK=180°,可得答案.
解答:
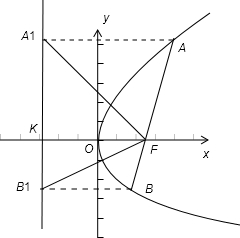 解:如图:设准线与x轴的交点为K,
解:如图:设准线与x轴的交点为K,
∵A、B在抛物线的准线上的射影为A1、B1,
由抛物线的定义可得,AA1=AF,
∴∠AA1F=∠AFA1,又由内错角相等得∠AA1F=∠A1FK,
∴∠AFA1=∠A1FK.
同理可证∠BFB1=∠B1 FK.
由∠AFA1+∠A1FK+∠BFB1+∠B1FK=180°,
∴∠A1FK+∠B1FK=∠A1FB1=90°,
故答案为:90°
 解:如图:设准线与x轴的交点为K,
解:如图:设准线与x轴的交点为K,∵A、B在抛物线的准线上的射影为A1、B1,
由抛物线的定义可得,AA1=AF,
∴∠AA1F=∠AFA1,又由内错角相等得∠AA1F=∠A1FK,
∴∠AFA1=∠A1FK.
同理可证∠BFB1=∠B1 FK.
由∠AFA1+∠A1FK+∠BFB1+∠B1FK=180°,
∴∠A1FK+∠B1FK=∠A1FB1=90°,
故答案为:90°
点评:本题的考点是抛物线的简单性质,主要考查抛物线的定义,考查两条直线平行,内错角相等,其中推出∠AFA1=∠A1FK是解题的关键.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
今年4月20日8:30分四川芦山发生强地震,得知此消息,某医院决定从4名内科和6名外科医生(包含一名骨外科专家)10名医生中,用分层抽样的方式组成一个5人的医疗小组赶赴灾区展开震后的救护工作,则骨外科专家被选派的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知f1(x)=sinx-cosx,fn+1(x)是fn(x)的导函数,即f2(x)=f1′(x),f3(x)=f2′(x),…,fn+1(x)=fn′(x),n∈N*,则f2013(x)=( )
| A、sinx+cosx |
| B、sinx-cosx |
| C、-sinx+cosx |
| D、-sinx-cosx |
在极坐标系中,圆C的圆心为(6,
),半径为5,直线θ=α(0≤α≤
,ρ∈R)被圆截得的弦长为8,则α的值为( )
| π |
| 2 |
| π |
| 2 |
A、
| ||
B、
| ||
C、
| ||
| D、以上都不对 |
极坐标方程4ρsin2
=5表示的曲线为( )
| θ |
| 2 |
| A、直线 | B、圆 | C、椭圆 | D、抛物线 |
“双曲线的方程为
-
=1”是“双曲线的渐近线方程为y=±
x”的( )
| x2 |
| 9 |
| y2 |
| 16 |
| 4 |
| 3 |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
用秦九韶算法求多项式f(x)=7x6+6x5+3x2+2当x=4的值时,第一步算的是( )
| A、4×4=16 |
| B、7×4=28 |
| C、4×4×4=64 |
| D、7×4+6=34 |
设A=
,B=
,则A与B的大小关系是( )
| x+1 |
| x+2 |
| x+3 |
| x+4 |
| A、A<B |
| B、A>B |
| C、仅有x>0,A<B |
| D、以上结论都不成立 |