题目内容
已知直线l1：mx+4y-m-2=0，l2：x+my-m=0，实数m为何值时，l1与l2：
（1）相交；
（2）平行；
（3）重合．
（1）相交；
（2）平行；
（3）重合．
考点：直线的一般式方程
专题：直线与圆
分析：（1）利用两条直线相交时，由方程组得到的一次方程有唯一解，一次项的系数不等于0．
（2）利用两直线平行时，一次项系数之比相等，但不等于常数项之比，求出m的值．
（3）利用两直线重合时，一次项系数之比等于常数项之比，求出m的值．
（2）利用两直线平行时，一次项系数之比相等，但不等于常数项之比，求出m的值．
（3）利用两直线重合时，一次项系数之比等于常数项之比，求出m的值．
解答：
解：（1）当l1和l2相交时，1×4-m2≠0，
由4-m2=0得：m=-2，或m=2，
∴当m≠-2且m≠2时，l1和l2相交．
（2）当m=-2时，直线l1：mx+4y-m-2=0，l2：x+my-m=0可化为：直线l1：-2x+4y=0，l2：x-2y+2=0，
此时一次项系数之比相等，但不等于常数项之比，两直线平行；
（3）当m=2时，直线l1：mx+4y-m-2=0，l2：x+my-m=0可化为：直线l1：2x+4y-4=0，l2：x+2y-2=0，
此时一次项系数之比等于常数项之比，两直线重合
由4-m2=0得：m=-2，或m=2，
∴当m≠-2且m≠2时，l1和l2相交．
（2）当m=-2时，直线l1：mx+4y-m-2=0，l2：x+my-m=0可化为：直线l1：-2x+4y=0，l2：x-2y+2=0，
此时一次项系数之比相等，但不等于常数项之比，两直线平行；
（3）当m=2时，直线l1：mx+4y-m-2=0，l2：x+my-m=0可化为：直线l1：2x+4y-4=0，l2：x+2y-2=0，
此时一次项系数之比等于常数项之比，两直线重合
点评：本题考查两直线相交、重合、平行的条件，体现了转化的数学思想．
练习册系列答案
相关题目
已知θ∈R时，不等式m2-（1+4sin2θ）m+4-6cos2θ≥0恒成立，则实数m的取值范围是（ ）
| A、m≥4或m≤1 |
| B、m≥4或m≤-1 |
| C、m≥2或m≤1 |
| D、m≥2或m≤-1 |
某种商品若每个售价60元，则可卖出50个；已知单价每提高10元，则少卖5个，要得到最大的售货金额，售价应定为（ ）
| A、80元 | B、85元 |
| C、90元 | D、100元 |
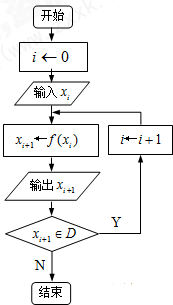对任意函数f（x），x∈D，可按如图构造一个数列发生器，由数列发生器产生的数列记为{xn}．