题目内容

设复数z满足（z+i）（1+i）=1-i（i是虚数单位），则|z|=（　　）
A、1B、2C、3D、4
考点：复数求模
专题：数系的扩充和复数
分析：变形已知条件可得z+i=
1-i
1+i
，化简可得z，可得模长．
解答： 解：∵（z+i）（1+i）=1-i，
∴z+i=
1-i
1+i
=
(1-i)2
(1+i)(1-i)

=
-2i
2
=-i，∴z=-2i
∴|z|=2
故选：B．
点评：本题考查复数的代数形式的运算，涉及模长的求解，属基础题．
练习册系列答案
相关题目
若二项式（x2-
2
x
）n的展开式中二项式系数的和是64，则展开式中的常数项为
 
．
已知函数f（x）=
k(x-1)+1，x≤1
ln(x-1)，x＞1
，则当k＜0时函数y=f（f（x））有
 
个零点．
已知向量
a
，
b
满足|
a
|=1，
b
=（1，-
3
），且
a
⊥（
a
+
b
），则
a
与
b
的夹角为（　　）
A、60°B、90°
C、120°D、150°
命题“?∈R，使x5+1＜0”的否定是（　　）
A、?x∈R，使x5+1≥0
B、?x∈R，使x5+1＞0
C、?x∈R，使x5+1＞0
D、?x∈R，使x5+1≥0
已知cos（α-
π
4
）=
1
4
，则sin2α的值为（　　）
A、
7
8
B、-
7
8
C、
3
4
D、-
3
4
已知sinθ＜0，cosθ＜0，则角θ的终边所在的象限是（　　）
A、第一象限B、第二象限
C、第三象限D、第四象限
函数y=|2x-1|的大致图象是（　　）
A、
B、
C、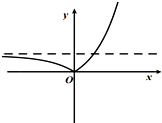
D、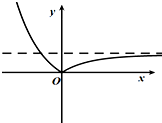
若二次不等式 ax2+bx+6＜0 的解集是{x|x＜-2或x＞3}，则a=（　　）
A、2B、-2C、1D、-1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网