题目内容

圆（x-1）2+（y+2）2=5的圆心坐标为（　　）
A、（1，2）
B、（1，-2）
C、（-1，2）
D、（-1，-2）
考点：圆的标准方程
专题：直线与圆
分析：由条件利用圆的标准方程特征可得圆（x-1）2+（y+2）2=5的圆心坐标．
解答： 解：根据圆的标准方程特征可得圆（x-1）2+（y+2）2=5的圆心坐标为（1，-2），
故选：B．
点评：本题主要考查圆的标准方程特征，属于基础题．
练习册系列答案
相关题目
已知函数f（x）=
k(x-1)+1，x≤1
ln(x-1)，x＞1
，则当k＜0时函数y=f（f（x））有
 
个零点．
已知sinθ＜0，cosθ＜0，则角θ的终边所在的象限是（　　）
A、第一象限B、第二象限
C、第三象限D、第四象限
函数y=|2x-1|的大致图象是（　　）
A、
B、
C、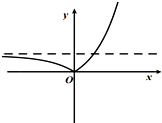
D、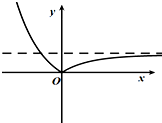
曲线
x2
sinθ+3
+
y2
sinθ-2
=1所表示的图形是（　　）
A、焦点在x轴上的椭圆
B、焦点在y轴上的双曲线
C、焦点在x轴上的双曲线
D、焦点在y轴上的椭圆
在△ABC中，a2+c2-b2=
3
ac，则∠B=（　　）
A、60°B、45°
C、120°D、30°
在△ABC中，角A，B，C的对边分别是a，b，c，且a＞b＞c，如果a2＜b2+c2，则A的取值范围是（　　）
A、90°＜A＜180°
B、45°＜A＜90°
C、60°＜A＜90°
D、0°＜A＜90°
若二次不等式 ax2+bx+6＜0 的解集是{x|x＜-2或x＞3}，则a=（　　）
A、2B、-2C、1D、-1
已知变量x与y之间的回归直线方程为y=-3+2x，若
10
i=1
xi=17，则
10
i=1
yi的值等于（　　）
A、3B、4C、0.4D、40

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网