题目内容
设点M在曲线y=ex上,点N在曲线y=1-
(x>0)上,则|MN|的最小值为 .
| 1 |
| x |
考点:函数与方程的综合运用
专题:计算题,导数的概念及应用
分析:求两个曲线上不同两点的距离的最小值,显然没法利用两点间的距离公式计算,可结合函数y=ex上的点关于y=x的对称点在其反函数的图象上把问题转化为求曲线y=lnx上的点与y=1-
(x>0)上的点到直线y=x的距离之和最小问题,而与y=x平行的直线同时与曲线y=lnx和y=1-
(x>0)切于同一点(1,0),所以PQ的距离的最小值为(1,0)点到直线y=x距离的2倍.
| 1 |
| x |
| 1 |
| x |
解答:
解:曲线y=ex与曲线y=lnx互为反函数,其图象关于y=x对称,
设函数f(x)=lnx-(1-
),则f′(x)=
-
=
,
∴当0<x<1时,f′(x)<0,x>1时,f′(x)>0,
∴函数f(x)在(0,+∞)上有最小值f(1)=0,
∴当x>0时,除(1,0)点外函数y=lnx的图象恒在y=1-
的上方,在(1,0)处两曲线相切.
求曲线y=ex上的点M与曲线y=1-
(x>0)上的点N的距离的最小值,可看作是求曲线y=lnx上的点M′与N点到直线y=x的距离的最小值的和,而函数y=lnx与y=1-
(x>0)在x=1时的导数都是1,说明与直线y=x平行的直线与两曲线切于同一点(1,0),则MN的距离的最小值为(1,0)点到直线y=x距离的2倍,
∴|MN|的最小值为2•
=
.
故答案为:
.
设函数f(x)=lnx-(1-
| 1 |
| x |
| 1 |
| x |
| 1 |
| x2 |
| x-1 |
| x2 |
∴当0<x<1时,f′(x)<0,x>1时,f′(x)>0,
∴函数f(x)在(0,+∞)上有最小值f(1)=0,
∴当x>0时,除(1,0)点外函数y=lnx的图象恒在y=1-
| 1 |
| x |
求曲线y=ex上的点M与曲线y=1-
| 1 |
| x |
| 1 |
| x |
∴|MN|的最小值为2•
| 1 | ||
|
| 2 |
故答案为:
| 2 |
点评::本题考查了两点间的距离,考查了数形结合的解题思想,考查了数学转化思想,解答此题的关键是分析得到函数y=lnx的图象除(1,0)点外恒在y=1-
的上方,且在(1,0)处两曲线相切.此题属于中档题.
| 1 |
| x |

练习册系列答案
相关题目
已知向量
,
满足|
|=1,
=(1,-
),且
⊥(
+
),则
与
的夹角为( )
| a |
| b |
| a |
| b |
| 3 |
| a |
| a |
| b |
| a |
| b |
| A、60° | B、90° |
| C、120° | D、150° |
函数y=|2x-1|的大致图象是( )
A、 |
B、 |
C、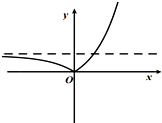 |
D、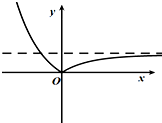 |

