题目内容
| sinα+cosα |
| sinα-cosα |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
考点:三角函数的化简求值
专题:三角函数的求值
分析:由已知先求tanα,把所求的式子中的三角函数利用二倍角公式进行化简,然后化为正切形式,代入可求 值
解答:
解:∵
=3,∴sinα=2cosα,
∴tanα=2,
则sin2α+sinαcosα=
=
=
=
.
故选:D.
| sinα+cosα |
| sinα-cosα |
∴tanα=2,
则sin2α+sinαcosα=
| sin2α+sinαcosα |
| sin2α+cos2α |
| tan2α+tanα |
| tan2α+1 |
| 22+2 |
| 22+1 |
| 6 |
| 5 |
故选:D.
点评:此题考查了二倍角的正弦、余弦函数公式,以及同角三角函数间的基本关系,熟练掌握二倍角的正弦、余弦函数公式是解本题的关键.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
函数y=|2x-1|的大致图象是( )
A、 |
B、 |
C、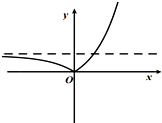 |
D、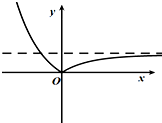 |
若二次不等式 ax2+bx+6<0 的解集是{x|x<-2或x>3},则a=( )
| A、2 | B、-2 | C、1 | D、-1 |
关于曲线的对称性的论述正确的是( )
| A、方程x2+xy+y2=0的曲线关于X轴对称 |
| B、方程x3+y3=0的曲线关于Y轴对称 |
| C、方程x2-xy+y2=10的曲线关于原点对称 |
| D、方程x3-y3=8的曲线关于原点对称 |
用数字0、1、2、3能组成多少个没有重复数字的四位偶数( )
| A、6 | B、10 | C、12 | D、24 |
三个实数a,b,c依次成公差不为零的等差数列,且a,c,b成等比数列,则
的值是( )
| a |
| b |
| A、-2 | B、2 | C、4 | D、-4 |
已知变量x与y之间的回归直线方程为y=-3+2x,若
xi=17,则
yi的值等于( )
| 10 |
 |
| i=1 |
| 10 |
 |
| i=1 |
| A、3 | B、4 | C、0.4 | D、40 |