题目内容
7.下列命题正确的个数是( )①$\overrightarrow{AB}+\overrightarrow{BA}=\overrightarrow 0$
②$\overrightarrow 0•\overrightarrow{AB}=\overrightarrow 0$
③$\overrightarrow a与\overrightarrow b$共线,则$\overrightarrow a•\overrightarrow b=|{\overrightarrow a}||{\overrightarrow b}|$
④$(\overrightarrow a•\overrightarrow b)•\overrightarrow c=\overrightarrow a•(\overrightarrow b\overrightarrow{•c})$.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据向量加法的几何意义,数量积的定义,共线向量的定义,以及向量数乘的几何意义即可判断每个命题的正误,从而找出正确选项.
解答 解:①$\overrightarrow{AB}=-\overrightarrow{BA}$;
∴$\overrightarrow{AB}+\overrightarrow{BA}=-\overrightarrow{BA}+\overrightarrow{BA}=\overrightarrow{0}$;
∴该命题正确;
②数量积是一个实数,不是向量;
∴该命题错误;
③$\overrightarrow{a}$与$\overrightarrow{b}$共线,且方向相反时,$\overrightarrow{a}•\overrightarrow{b}=-|\overrightarrow{a}||\overrightarrow{b}|$;
∴该命题错误;
④$\overrightarrow{c}$与$\overrightarrow{a}$不共线,且$\overrightarrow{a}•\overrightarrow{b}≠0,\overrightarrow{b}•\overrightarrow{c}≠0$时,$(\overrightarrow{a}•\overrightarrow{b})•\overrightarrow{c}≠\overrightarrow{a}•(\overrightarrow{b}•\overrightarrow{c})$;
∴该命题错误;
∴正确命题的个数为1.
故选A.
点评 考查向量加法和数乘的几何意义,以及数量积和共线向量的定义.

练习册系列答案
相关题目
18.已知集合A={x|ax2+x-3=0},B={x|3≤x<7},若A∩B≠∅,则实数a的取值集合为( )
| A. | $[-\frac{1}{12},-\frac{4}{49})$ | B. | $[-\frac{1}{12},0]$ | C. | $(-\frac{4}{49},0]$ | D. | $[-\frac{4}{49},0]$ |
15.已知x,y为正实数,且x+y+$\frac{1}{x}$+$\frac{1}{y}$=5,则x+y的最大值是( )
| A. | 3 | B. | $\frac{7}{2}$ | C. | 4 | D. | $\frac{9}{2}$ |
16.过抛物线y=2x2的焦点F作倾斜角为120°的直线交抛物线于A、B两点,则弦|AB|的长为( )
| A. | 2 | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | 1 |
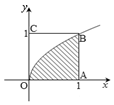 如图,在正方形OABC内任取一点,取到函数$y=\sqrt{x}$的图象与x轴正半轴之间
如图,在正方形OABC内任取一点,取到函数$y=\sqrt{x}$的图象与x轴正半轴之间