如图.在正方形OABC内任取一点.取到函数$y=\sqrt{x}$的图象与x轴正半轴之间的点的概率等于$\frac{2}{3}$．题目和参考答案——青夏教育精英家教网——

题目内容

2．

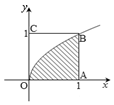如图，在正方形OABC内任取一点，取到函数$y=\sqrt{x}$的图象与x轴正半轴之间
（阴影部分）的点的概率等于$\frac{2}{3}$．

分析欲求所投的点落在阴影部分内部的概率，须结合定积分计算阴影部分平面区域的面积，再根据几何概型概率计算公式易求解．

解答解：根据题意，正方形OABC的面积为1×1=1，阴影部分的面积为${∫}_{0}^{1}$$\sqrt{x}$dx=$\frac{2}{3}{x}^{\frac{3}{2}}$|${\;}_{0}^{1}$=$\frac{2}{3}$，
由几何概型的概率公式得，点落在阴影部分的概率为P=$\frac{2}{3}$．
故答案为$\frac{2}{3}$．

点评本题考查几何概型的计算，涉及定积分在求面积中的应用，关键是正确计算出阴影部分的面积．

练习册系列答案

金榜夺冠真题卷系列答案

小升初综合素质检测卷系列答案

琢玉计划暑假系列答案

小升初重点校各地真题精编卷系列答案

万唯教育非常九年级系列答案

应用题作业本系列答案

起跑线系列丛书新课标暑假作业系列答案

师大卷王决胜期末100分系列答案

望子成龙最新小学毕业升学必备系列答案

小学升小学毕业升学系统总复习系列答案

相关题目

12．已知定义在R上的函数f（x）为周期函数，且周期为4，若在区间[-2，2]上，f（x）=$\left\{\begin{array}{l}{{2}^{x}+2m，-2≤x≤0}\\{lo{g}_{2}x-m，0＜x≤2}\end{array}\right.$，则f（2017m）=（　　）

13．抛物线x=4y²的焦点坐标是（　　）

$（{-\frac{1}{16}，0}）$

$（{\frac{1}{16}，0}）$

10．已知函数$f（\frac{x}{2}）=-\frac{1}{8}{x^{\;}}+\frac{m}{4}{x^2}-m，g（x）=-\frac{1}{2}{x^3}+m{x^2}+（a+1）x+2xcosx-m$．
（1）若曲线y=f（x）仅在两个不同的点A（x₁，f（x₁）），B（x₂，f（x₂））处的切线都经过点（2，t），
求证：t=3m-8或$t=-\frac{1}{27}{m^3}+\frac{2}{3}{m^2}-m$；
（2）当x∈[0，1]时，若f（x）≥g（x）恒成立，求a的取值范围．

把正偶数数列{2n}的各项从小到大依次排成如图的三角形数阵，记M（r，t）表示该数阵中第r行的第t个数，则数阵中的数2 012对应于第45行的第16个数．

7．下列命题正确的个数是（　　）
①$\overrightarrow{AB}+\overrightarrow{BA}=\overrightarrow 0$
②$\overrightarrow 0•\overrightarrow{AB}=\overrightarrow 0$
③$\overrightarrow a与\overrightarrow b$共线，则$\overrightarrow a•\overrightarrow b=|{\overrightarrow a}||{\overrightarrow b}|$
④$（\overrightarrow a•\overrightarrow b）•\overrightarrow c=\overrightarrow a•（\overrightarrow b\overrightarrow{•c}）$．

14．设f（x）=x•lnx，若$f'（{x_0}）=\frac{3}{2}$，则x₀=（　　）

$\frac{1}{e^2}$

11．若函数$f（x）=\sqrt{{2^{a{x^2}-2ax-1}}-1}$的定义域为R，则实数a的取值范围是∅．

12．已知直线l的参数方程是$\left\{\begin{array}{l}{x=\frac{\sqrt{2}}{2}t}\\{y=\frac{\sqrt{2}}{2}t+4\sqrt{2}}\end{array}\right.$（t是参数），圆C的极坐标方程为ρ=4cos（θ+$\frac{π}{4}$）．
（Ⅰ）求圆心C的直角坐标；
（Ⅱ）由直线l上的点向圆C引切线，求切线长的最小值．