��Ŀ����
12��һ���ڴ���װ�д�С��״��ȫ��ͬ��n+3��ƹ��������1��ƹ�����ϱ�������1��2��ƹ�����ϱ�������2������n��ƹ�����Ͼ���������3��n��N*������������ڴ������������2��ƹ����ǡ��һ��ƹ�����ϱ�������2�ĸ�����$\frac{8}{15}$����1����n��ֵ��
��2���ӿڴ������������2��ƹ������α�ʾ��������2��ƹ��������������֮�ͣ���εķֲ��к���ѧ����E����
���� ��1���������������г��������n��ֵ��
��2��������֪��ȡֵΪ3��4��5��6�������Ӧ�ĸ���ֵ��д���εķֲ��к���ѧ����ֵ��
��� �⣺��1��������֪��$\frac{{C}_{n+1}^{1}{•C}_{2}^{1}}{{C}_{n+3}^{2}}$=$\frac{8}{15}$��
������2n2-5n-3=0��
���n=3��n=-$\frac{1}{2}$���������⣬��ȥ����
��n=3��
��2��������֪��ȡֵΪ3��4��5��6��
P����=3��=$\frac{{C}_{1}^{1}{•C}_{2}^{1}}{{C}_{6}^{2}}$=$\frac{2}{15}$��
P����=4��=$\frac{{C}_{2}^{2}{+C}_{1}^{1}{•C}_{3}^{1}}{{C}_{6}^{2}}$=$\frac{4}{15}$��
P����=5��=$\frac{{C}_{2}^{1}{•C}_{3}^{1}}{{C}_{6}^{2}}$=$\frac{6}{15}$=$\frac{2}{5}$��
P����=6��=$\frac{{C}_{3}^{2}}{{C}_{6}^{2}}$=$\frac{3}{15}$=$\frac{1}{5}$��
��εķֲ���Ϊ��
| �� | 3 | 4 | 5 | 6 |
| P | $\frac{2}{15}$ | $\frac{4}{15}$ | $\frac{2}{5}$ | $\frac{1}{5}$ |
���� ���⿼����ɢ����������ķֲ��к���ѧ�����������⣬����ʱҪע���������֪ʶ�ĺ������ã����ۺ��⣮

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
20������$z=\frac{-2+2i}{1+i}$�Ĺ�����ǣ�������
| A�� | 1+i | B�� | 1-i | C�� | 2i | D�� | -2i |
17��������f��x��=5cos��wx+�գ�������ʵ��x������$f��\frac{��}{3}+x��=f��\frac{��}{3}-x��$������g��x��=4sin��wx+�գ�+1��$g��\frac{��}{3}��$=��������
| A�� | 1 | B�� | 5 | C�� | -3 | D�� | 0 |
4����֪����Բ$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�����ҽ���F����б��120���ֱ��l����ԲΪA��B����$\overrightarrow{AF}$=2$\overrightarrow{FB}$������Բ��������Ϊ��������
| A�� | $\frac{1}{3}$ | B�� | $\frac{1}{2}$ | C�� | $\frac{\sqrt{2}}{2}$ | D�� | $\frac{2}{3}$ |
1����֪���ʣ�0���У�����sin��+cos��=$\frac{\sqrt{3}}{3}$����cos2��-sin2��=��������
| A�� | -$\frac{\sqrt{5}}{3}$ | B�� | -$\frac{\sqrt{2}}{3}$ | C�� | $\frac{\sqrt{5}}{3}$ | D�� | $\frac{\sqrt{2}}{3}$ |
2��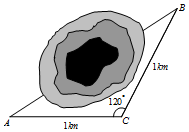 ��ͼ���ڸ��ٹ�·��������Ҫȷ�������ij��ȣ����̼�����Ա�Ѳ���������˵�����A��B����C�ľ���AC=BC=1km���ҡ�ACB=120�㣬��A��B�����ľ���Ϊ��������
��ͼ���ڸ��ٹ�·��������Ҫȷ�������ij��ȣ����̼�����Ա�Ѳ���������˵�����A��B����C�ľ���AC=BC=1km���ҡ�ACB=120�㣬��A��B�����ľ���Ϊ��������
 ��ͼ���ڸ��ٹ�·��������Ҫȷ�������ij��ȣ����̼�����Ա�Ѳ���������˵�����A��B����C�ľ���AC=BC=1km���ҡ�ACB=120�㣬��A��B�����ľ���Ϊ��������
��ͼ���ڸ��ٹ�·��������Ҫȷ�������ij��ȣ����̼�����Ա�Ѳ���������˵�����A��B����C�ľ���AC=BC=1km���ҡ�ACB=120�㣬��A��B�����ľ���Ϊ��������| A�� | $\sqrt{3}$km | B�� | $\sqrt{2}$km | C�� | 1.5km | D�� | 2km |