题目内容

17．△ABC中，角A，B，C所对的边分别为a，b，c，且2sin Acos B+sinB=2sin C．
（1）求角A；
（2）若a=4$\sqrt{3}$，b+c=8，求△ABC 的面积．

分析 （1）利用和角的三角函数，即可求角A；
（2）若a=4$\sqrt{3}$，b+c=8，求出bc，即可求△ABC 的面积．

解答 解：（1）∵2sin Acos B+sinB=2sin C，
∴2sin Acos B+sinB=2sin （A+B）
得2sin Acos B+sinB=2sinAcosB+2cosAsinB，
∴cosA=$\frac{1}{2}$，
∵0°＜A＜180°，
∴A=60°．
（2）由余弦定理48=b2+c2-bc
b+c=8，配方得64-3bc=48，得bc=$\frac{16}{3}$，
∴△ABC 的面积S=$\frac{1}{2}bcsinA$=$\frac{4\sqrt{3}}{3}$．

点评 本题考查三角形面积的计算，考查余弦定理，考查学生的计算能力，属于中档题．

练习册系列答案
相关题目
7．下列命题正确的个数是（　　）
①$\overrightarrow{AB}+\overrightarrow{BA}=\overrightarrow 0$
②$\overrightarrow 0•\overrightarrow{AB}=\overrightarrow 0$
③$\overrightarrow a与\overrightarrow b$共线，则$\overrightarrow a•\overrightarrow b=|{\overrightarrow a}||{\overrightarrow b}|$
④$（\overrightarrow a•\overrightarrow b）•\overrightarrow c=\overrightarrow a•（\overrightarrow b\overrightarrow{•c}）$．
A．1B．2C．3D．4
8．若实数x，y满足$\left\{\begin{array}{l}{y≤2}\\{|x|-y+1≤0}\end{array}\right.$，则z=$\frac{y+2}{x-2}$的最小值为4．
5．已知x2+y2-4x-2y-4=0，则$\frac{2x+3y+1}{x+2}$的最小值是（　　）
A．-2B．$-\frac{17}{4}$C．$-\frac{29}{5}$D．$2-\frac{{9\sqrt{7}}}{7}$
12．已知直线l的参数方程是$\left\{\begin{array}{l}{x=\frac{\sqrt{2}}{2}t}\\{y=\frac{\sqrt{2}}{2}t+4\sqrt{2}}\end{array}\right.$（t是参数），圆C的极坐标方程为ρ=4cos（θ+$\frac{π}{4}$）．
（Ⅰ）求圆心C的直角坐标；
（Ⅱ）由直线l上的点向圆C引切线，求切线长的最小值．
2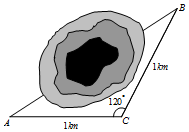．如图，在高速公路建设中需要确定隧道的长度，工程技术人员已测得隧道两端的两点A、B到点C的距离AC=BC=1km，且∠ACB=120°，则A、B两点间的距离为（　　）
A．$\sqrt{3}$kmB．$\sqrt{2}$kmC．1.5kmD．2km
9．已知椭圆$C：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的短轴长为2，离心率$e=\frac{{\sqrt{3}}}{2}$．
（1）求椭圆的标准方程；
（2）直线l：y=x+m与椭圆C交于不同的两点A，B，若∠AOB为锐角，求实数m的取值范围．
6．（1）计算定积分$\int_{-4}^3{|x+2|}dx$
（2）求由曲线y=x2+2与y=3x，x=0，x=2所围成的平面图形的面积．
7．在等腰梯形ABCD中，AB∥CD，AB=4，CD=2，∠A=60°，G为对角线AC上一点，且$\overrightarrow{AG}•\overrightarrow{AB}$=6，过G的直线分别交两腰AD，BC于M，N两点，若$\overrightarrow{AC}$=m$\overrightarrow{AM}+n\overrightarrow{AN}$，则$\frac{1}{m}+\frac{1}{n+1}$的最小值为$\frac{4}{3}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网