题目内容
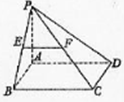 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AP=AB,E,F分别是PB,PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AP=AB,E,F分别是PB,PC的中点.(Ⅰ)证明:EF∥平面PAD;
(Ⅱ)求证:AE⊥PC.
考点:直线与平面平行的判定,空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:(Ⅰ)先证明出EF∥AD,进而根据线面平行的判定定理证明出EF∥平面PAD
(Ⅱ)先根据线面垂直的判定定理证明出BC⊥平面PAB,进而根据线面垂直的性质推断出AE⊥BC,然后根据线面垂直的判定定理证明出AE⊥平面PBC,则AE⊥PC得证.
(Ⅱ)先根据线面垂直的判定定理证明出BC⊥平面PAB,进而根据线面垂直的性质推断出AE⊥BC,然后根据线面垂直的判定定理证明出AE⊥平面PBC,则AE⊥PC得证.
解答:
(Ⅰ)证明:∵E,F分别是PB,PC的中点,
∴EF∥BC,
∵BC∥AD,
∴EF∥AD,
∵EF?平面PAD,AD?平面PAD,
∴EF∥平面PAD.
(Ⅱ) 证明:∵AP=AB,E是PB的中点,
∴AE⊥PB,
∵PA⊥平面ABCD,
∴PA⊥BC,
∵AB⊥BC且PA∩AB=A,
∴BC⊥平面PAB,
∵AE?平面PAB,
∴AE⊥BC,
∵PB∩BC=B,
∴AE⊥平面PBC,
∴AE⊥PC.
∴EF∥BC,
∵BC∥AD,
∴EF∥AD,
∵EF?平面PAD,AD?平面PAD,
∴EF∥平面PAD.
(Ⅱ) 证明:∵AP=AB,E是PB的中点,
∴AE⊥PB,
∵PA⊥平面ABCD,
∴PA⊥BC,
∵AB⊥BC且PA∩AB=A,
∴BC⊥平面PAB,
∵AE?平面PAB,
∴AE⊥BC,
∵PB∩BC=B,
∴AE⊥平面PBC,
∴AE⊥PC.
点评:本题主要考查了线面平行和线面垂直的判定定理的应用.考查了学生空间观察能力和推理能力.

练习册系列答案
相关题目
设(x+1)(2x+1)10=a0+a1(x+2)+a2(x+2)2+…+a11(x+2)11,则a1+a2+a3+…+a11的值是( )
| A、-310 |
| B、0 |
| C、310 |
| D、510 |
 如图,已知椭圆C:
如图,已知椭圆C: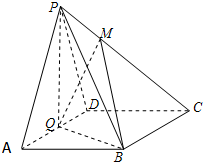 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点,点M在线段PC上,MC=2PM.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点,点M在线段PC上,MC=2PM.