题目内容
在平面直角坐标系xOy中，设动点P，Q都在曲线C：
（θ为参数）上，且这两点对应的参数分别为θ=α与θ=2α（0＜α＜2π），设PQ的中点M与定点A（1，0）间的距离为d，求d的取值范围．
|
考点：简单曲线的极坐标方程
专题：坐标系和参数方程
分析：设出P、Q的坐标，即P （ 1+2cosα，2sinα ），Q （ 1+2cos2α，sin2α ），则PQ的中点M为（1+cosα+cos2α，sinα+sin2α），再根据两点间距离公式求解．
解答：
解：由题设可知P （ 1+2cosα，2sinα ），Q （ 1+2cos2α，sin2α ），
于是PQ的中点M（1+cosα+cos2α，sinα+sin2α）．
从而d2=MA2=（cosα+cos2α）2+（sinα+sin2α）2=2+2cosα，
因为0＜α＜2π，所以-1≤cosα＜1，
于是0≤d 2＜4，故d的取值范围是[0，2）．
于是PQ的中点M（1+cosα+cos2α，sinα+sin2α）．
从而d2=MA2=（cosα+cos2α）2+（sinα+sin2α）2=2+2cosα，
因为0＜α＜2π，所以-1≤cosα＜1，
于是0≤d 2＜4，故d的取值范围是[0，2）．
点评：在求解与参数相关的题目时要注意参数范围的限制，例如本题中“0＜α＜2π”，从而得到“-1≤cosα＜1”．
练习册系列答案
相关题目
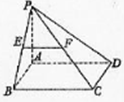如图，在四棱锥P-ABCD中，底面ABCD是矩形，PA⊥平面ABCD，AP=AB，E，F分别是PB，PC的中点．
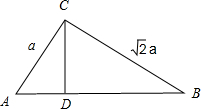在Rt△ABC中，两直角边的长分别为AC=a，BC=