题目内容
已知直线l，平面α、β，若l⊥α，l⊥β，求证：α∥β．
考点：平面与平面平行的判定
专题：证明题,空间位置关系与距离
分析：过l作辅助平面γ与α、β分别交于a，a′，证明a∥β，同理可得b∥β，a∩b=O，利用面面平行的判定定理可得α∥β．
解答：
证明：过l作辅助平面γ与α、β分别交于a，a′
∵l⊥α，l⊥β，
∴l⊥a，l⊥a′，
∴a∥a′
∵a?α，a′?β，
∴a∥β，
同理过l作辅助平面γ与α、β分别交于b，b′，可得b∥β，
设a∩b=O，
∴α∥β．
∵l⊥α，l⊥β，
∴l⊥a，l⊥a′，
∴a∥a′
∵a?α，a′?β，
∴a∥β，
同理过l作辅助平面γ与α、β分别交于b，b′，可得b∥β，
设a∩b=O，
∴α∥β．
点评：本题考查线面、面面平行的判定定理，考查学生分析解决问题的能力，比较基础．
练习册系列答案
相关题目
已知an=（| 1 |
| 3 |
A、（
| ||
B、（
| ||
C、（
| ||
D、（
|
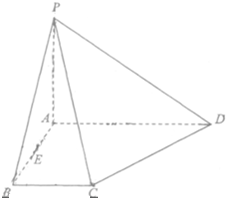如图，在四棱锥P-ABCD中，底面ABCD是直角梯形，且∠ABC=90°，AD∥BC，AD=2，AB=BC=1，PA⊥平面ABCD，E是线段AB的中点．
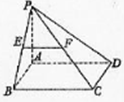如图，在四棱锥P-ABCD中，底面ABCD是矩形，PA⊥平面ABCD，AP=AB，E，F分别是PB，PC的中点．
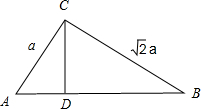在Rt△ABC中，两直角边的长分别为AC=a，BC=