题目内容
若a,b,c∈R+,且满足a+b+c=2.
(Ⅰ)求abc的最大值;
(Ⅱ)证明:
+
+
≥
.
(Ⅰ)求abc的最大值;
(Ⅱ)证明:
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| 9 |
| 2 |
考点:二维形式的柯西不等式
专题:选作题,不等式
分析:(Ⅰ)利用基本不等式,可求abc的最大值;
(Ⅱ)利用柯西不等式,即可证明.
(Ⅱ)利用柯西不等式,即可证明.
解答:
(Ⅰ)解:因为a,b,c∈R+,所以2=a+b+c≥3
,故abc≤
.….(3分)
当且仅当a=b=c=
时等号成立,所以abc的最大值为
.….(4分)
(Ⅱ)证明:因为a,b,c∈R+,且a+b+c=2,所以根据柯西不等式,
可得
+
+
=
(a+b+c)(
+
+
) ….(5分)
=
[(
)2+(
)2+(
)2][(
)2+(
)2+(
)2]≥
(
×
+
×
+
×
)2=
.
所以
+
+
≥
.….(7分)
| 3 | abc |
| 8 |
| 27 |
当且仅当a=b=c=
| 2 |
| 3 |
| 8 |
| 27 |
(Ⅱ)证明:因为a,b,c∈R+,且a+b+c=2,所以根据柯西不等式,
可得
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| 1 |
| 2 |
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
=
| 1 |
| 2 |
| a |
| b |
| c |
|
|
|
| 1 |
| 2 |
| a |
|
| b |
|
| c |
|
| 9 |
| 2 |
所以
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| 9 |
| 2 |
点评:本小题主要考查平均值不等式、柯西不等式等基础知识,考查推理论证能力,考查化归与转化思想.

练习册系列答案
相关题目
 如图,有一菱形纸片ABCD,∠A=60°,E是AD边上的一点(不包括A,D),先将ABCD沿对角线BD折成直二面角,再将△ABE沿BE翻折到△A′BE,下列不可能正确的是( )
如图,有一菱形纸片ABCD,∠A=60°,E是AD边上的一点(不包括A,D),先将ABCD沿对角线BD折成直二面角,再将△ABE沿BE翻折到△A′BE,下列不可能正确的是( )| A、BC与平面A′BE内某直线平行 |
| B、BC与平面A′BE内某直线垂直 |
| C、CD∥平面A′BE |
| D、CD⊥平面A′BE |
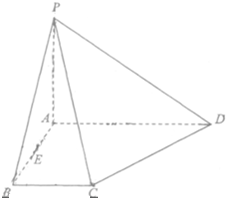 如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,且∠ABC=90°,AD∥BC,AD=2,AB=BC=1,PA⊥平面ABCD,E是线段AB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,且∠ABC=90°,AD∥BC,AD=2,AB=BC=1,PA⊥平面ABCD,E是线段AB的中点.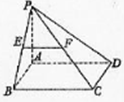 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AP=AB,E,F分别是PB,PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AP=AB,E,F分别是PB,PC的中点.