题目内容
设a＞b＞c＞0，则2a2+
+
-10ac+25c2取最小值时abc= ．
| 1 |
| ab |
| 1 |
| a(a-b) |
考点：基本不等式
专题：不等式的解法及应用
分析：把要求的式子变形后，利用基本不等式即可得出它的最小值，以及此时abc的值．
解答：
解：∵a＞b＞c＞0，2a2+
+
-10ac+25c2 =a2+[a2+
+
]-10ac+25c2
=[a2+
]+（a-5c）2≥a2+
+（a-5c）2=a2+
+（a-5c）2≥2
+0=4，
当且仅当a=2b=5c=
时取等号，
故答案为：4．
| 1 |
| ab |
| 1 |
| a(a-b) |
| 1 |
| ab |
| 1 |
| a(a-b) |
=[a2+
| 1 |
| b(a-b) |
| 1 | ||
(
|
| 4 |
| a2 |
a2•
|
当且仅当a=2b=5c=
| 2 |
故答案为：4．
点评：本题考查了基本不等式的性质，属于基础题．
练习册系列答案
相关题目
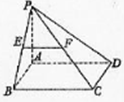如图，在四棱锥P-ABCD中，底面ABCD是矩形，PA⊥平面ABCD，AP=AB，E，F分别是PB，PC的中点．
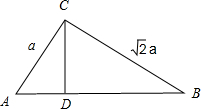在Rt△ABC中，两直角边的长分别为AC=a，BC=
如图，正方体ABCD-A1B1C1D1中，E，F分别是面A1B1C1D1和AA1D1D的中心，则EF和CD所成的角是