题目内容
设（x+1）（2x+1）10=a0+a1（x+2）+a2（x+2）2+…+a11（x+2）11，则a1+a2+a3+…+a11的值是（ ）
| A、-310 |
| B、0 |
| C、310 |
| D、510 |
考点：二项式系数的性质
专题：二项式定理
分析：在所给的等式中，令x=-2，可得 a0 的值．再令x=-1，可得a0+a1+a2+a3+…+a11=0，从而求得a1+a2+a3+…+a11的值．
解答：
解：在所给的等式中，令x=-2，可得 a0=-310．
再令x=-1，可得a0+a1+a2+a3+…+a11=0，
∴a1+a2+a3+…+a11=310，
故选：C．
再令x=-1，可得a0+a1+a2+a3+…+a11=0，
∴a1+a2+a3+…+a11=310，
故选：C．
点评：本题主要考查二项式定理的应用，是给变量赋值的问题，关键是根据要求的结果，选择合适的数值代入，属于基题．
练习册系列答案
相关题目
已知an=（| 1 |
| 3 |
A、（
| ||
B、（
| ||
C、（
| ||
D、（
|
设随机变量ξ～N（μ，σ2），且P（ξ≤c）=P（ξ＞c）=p，则p的值为：（ ）
| A、0 | B、0.5 | C、1 | D、不确定 |
如图，有一菱形纸片ABCD，∠A=60°，E是AD边上的一点（不包括A，D），先将ABCD沿对角线BD折成直二面角，再将△ABE沿BE翻折到△A′BE，下列不可能正确的是（ ）| A、BC与平面A′BE内某直线平行 |
| B、BC与平面A′BE内某直线垂直 |
| C、CD∥平面A′BE |
| D、CD⊥平面A′BE |
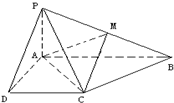已知四棱锥P-ABCD的底面为直角梯形，AB∥DC，∠DAB=90°，PA⊥底面ABCD，且PA=AD=DC=
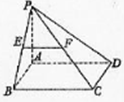如图，在四棱锥P-ABCD中，底面ABCD是矩形，PA⊥平面ABCD，AP=AB，E，F分别是PB，PC的中点．