题目内容
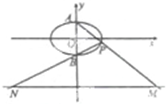 如图,已知椭圆C:
如图,已知椭圆C:| x2 |
| a2 |
| y2 |
| a2-1 |
| ||
| 2 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)证明:k1•k2为定值;
(Ⅲ)求直线MN长度的最小值.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由已知条件知e=
=
=
,由此能求出椭圆C的方程.
(Ⅱ)由椭圆方程求出两个顶点A,B的坐标,设出P点坐标,写出直线AP、BP的斜率k1,k2,结合P的坐标适合椭圆方程可证结论.
(Ⅲ)分别求出M和N点的坐标,由(Ⅱ)中的结论得到两直线斜率间的关系,把|MN|用含有一个字母的代数式表示,然后利用基本不等式求最值.
| c |
| a |
| 1 |
| a |
| ||
| 2 |
(Ⅱ)由椭圆方程求出两个顶点A,B的坐标,设出P点坐标,写出直线AP、BP的斜率k1,k2,结合P的坐标适合椭圆方程可证结论.
(Ⅲ)分别求出M和N点的坐标,由(Ⅱ)中的结论得到两直线斜率间的关系,把|MN|用含有一个字母的代数式表示,然后利用基本不等式求最值.
解答:
(Ⅰ)解:∵椭圆C:
+
=1的离心率为
,
∴e=
=
=
,解得a=
,
∴椭圆C的方程为
+y2=1.
(Ⅱ)证明:∵椭圆C的方程为
+y2=1.上、下顶点分别为A、B,点P在椭圆C上,
∴A(0,1),B(0,-1),设P(x0,y0),∵异于点A、B,∴x0≠0,
∴直线AP的斜率k1=
,直线BP的斜率k2=
,
∵P(x0,y0)在
+y2=1上,∴
+y02=1,x0≠0,
∴k1k2=
•
=
=
=-
.
∴k1•k2为定值-
.
(Ⅲ)解:由题意,直线AP:y-1=k1x,直线PB:y+1=k2x,
∵直线AP、BP与直线y=-3分别相交于点M、N,
∴由
,得M(-
,-3),
由
,刘N(-
,-3),
∴|MN|=|
-
|,又k1•k2=-
,∴k2=-
,
∴|MN|=|
+4k1|=
+4|k1|
≥2
=8.
当且仅当
=4|k1|,即k1=±1时,等号成立,
∴MN的最小值是8.
| x2 |
| a2 |
| y2 |
| a2-1 |
| ||
| 2 |
∴e=
| c |
| a |
| 1 |
| a |
| ||
| 2 |
| 2 |
∴椭圆C的方程为
| x2 |
| 2 |
(Ⅱ)证明:∵椭圆C的方程为
| x2 |
| 2 |
∴A(0,1),B(0,-1),设P(x0,y0),∵异于点A、B,∴x0≠0,
∴直线AP的斜率k1=
| y0-1 |
| x0 |
| y0+1 |
| x0 |
∵P(x0,y0)在
| x2 |
| 2 |
| x02 |
| 2 |
∴k1k2=
| y0-1 |
| x0 |
| y0+1 |
| x0 |
| y02-1 |
| x02 |
-
| ||
| x02 |
| 1 |
| 2 |
∴k1•k2为定值-
| 1 |
| 2 |
(Ⅲ)解:由题意,直线AP:y-1=k1x,直线PB:y+1=k2x,
∵直线AP、BP与直线y=-3分别相交于点M、N,
∴由
|
| 4 |
| k1 |
由
|
| 2 |
| k2 |
∴|MN|=|
| 4 |
| k1 |
| 2 |
| k2 |
| 1 |
| 2 |
| 1 |
| 2k1 |
∴|MN|=|
| 4 |
| k1 |
| 4 |
| |k1| |
≥2
|
当且仅当
| 4 |
| |k1| |
∴MN的最小值是8.
点评:本题考查了直线的斜率,考查了直线与圆锥曲线的关系,考查了利用基本不等式求最值,考查了椭圆方程,考查了学生的计算能力,是有一定难度题目.

练习册系列答案
相关题目
设随机变量ξ~N(μ,σ2),且P(ξ≤c)=P(ξ>c)=p,则p的值为:( )
| A、0 | B、0.5 | C、1 | D、不确定 |
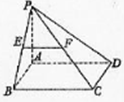 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AP=AB,E,F分别是PB,PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AP=AB,E,F分别是PB,PC的中点.