题目内容
17.函数y=sin(2x+$\frac{π}{12}$)的图象经过平移后所得图象关于点($\frac{π}{12}$,0)中心对称,这个平移变换可以是( )| A. | 向左平移$\frac{π}{8}$个单位 | B. | 向左平移$\frac{π}{4}$个单位 | ||
| C. | 向右平移$\frac{π}{8}$个单位 | D. | 向右平移$\frac{π}{4}$个单位 |
分析 利用函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象的对称性,得出结论.
解答 解:由于函数y=sin(2x+$\frac{π}{12}$)的图象的一个对称中心为(-$\frac{π}{24}$,0),
经过平移后所得图象关于点($\frac{π}{12}$,0)中心对称,
故这个平移变换可以是向右平移$\frac{π}{8}$个单位,
故选:C.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象的对称性,属于基础题.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
7.某车间加工零件的数量x与加工时间y的统计数据如表:
现已求得如表数据的回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$中的$\stackrel{∧}{b}$值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为102分钟.
| 零件数x(个) | 18 | 20 | 22 |
| 加工时间y(分钟) | 27 | 30 | 33 |
8.直线x-y-1=0的倾斜角与其在y轴上的截距分别是( )
| A. | 135°,1 | B. | 45°,-1 | C. | 45°,1 | D. | 135°,-1 |
12.若tan(α-β)=$\frac{1}{2}$,tan(α+β)=$\frac{1}{3}$,则tan2β等于( )
| A. | $\frac{1}{7}$ | B. | $\frac{4}{3}$ | C. | -$\frac{1}{7}$ | D. | -$\frac{4}{3}$ |
9.设函数f(x)在(-∞,+∞)上有意义,对于对定的正数k,定义函数fk(x)=$\left\{\begin{array}{l}{f(x),f(x)<k}\\{k,f(x)≥k}\end{array}\right.$取k=$\frac{1}{2}$,f(x)=($\frac{1}{2}$)|x|,则fk(x)=$\frac{k}{2}$的零点有( )
| A. | 0个 | B. | 1个 | ||
| C. | 2个 | D. | 不确定,随k的变化而变化 |
13.已知函数f(x)=Asin(ωx+φ)+B,(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图,则( )
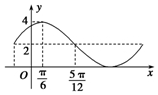

| A. | A=4 | B. | ω=1 | C. | φ=$\frac{π}{6}$ | D. | B=4 |
14.已知点M(-2,2)在抛物线C:y2=2px(p>0)的准线上,记抛物线C的焦点为F,则直线MF的方程为( )
| A. | x-2y+6=0 | B. | x+2y-2=0 | C. | 2x-y+6=0 | D. | 2x+y+2=0 |
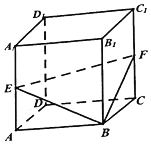 如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E,F分别是棱AA1,CC1的中点,P是侧面BCC1B1内一点,若A1P∥平面BEF,则线段A1P长度的取值范围是[$\frac{\sqrt{30}}{5}$,$\sqrt{2}$].
如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E,F分别是棱AA1,CC1的中点,P是侧面BCC1B1内一点,若A1P∥平面BEF,则线段A1P长度的取值范围是[$\frac{\sqrt{30}}{5}$,$\sqrt{2}$].