题目内容
12.若tan(α-β)=$\frac{1}{2}$,tan(α+β)=$\frac{1}{3}$,则tan2β等于( )| A. | $\frac{1}{7}$ | B. | $\frac{4}{3}$ | C. | -$\frac{1}{7}$ | D. | -$\frac{4}{3}$ |
分析 由条件利用两角差的正切公式,求得要求式子的值.
解答 解:∵tan(α-β)=$\frac{1}{2}$,tan(α+β)=$\frac{1}{3}$,则tan2β=tan[(α+β)-(α-β)]=$\frac{tan(α+β)-tan(α-β)}{1+tan(α+β)tan(α-β)}$=$\frac{\frac{1}{3}-\frac{1}{2}}{1+\frac{1}{3}•\frac{1}{2}}$=-$\frac{1}{7}$,
故选:C.
点评 本题主要考查两角差的正切公式的应用,属于基础题.

练习册系列答案
相关题目
2.下列说法正确的是( )
| A. | 在频率分布直方图中,众数左边和右边的直方图的面积相等 | |
| B. | 为调查高三年级的240名学生完成作业所需的时间,由教务处对高三年级的学生进行编号,从001到240抽取学号最后一位为3的学生进行调查,则这种抽样方法为分层抽样 | |
| C. | “x≠1”是“x2-3x+2≠0”的充分不必要条件 | |
| D. | 命题p:“?x0∈R,${x_0}^2-3{x_0}+2<0$”的否定为:“?x∈R,x2-3x+2≥0” |
20.设直线l与椭圆$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{8}=1$相交于A,B两点,与圆(x-1)2+y2=r2(r>0)相切于点M,且M为线段AB的中点,若这样的直线l恰有4条,则r的取值范围是( )
| A. | (1,$\sqrt{6}$) | B. | (2,$\sqrt{7}$) | C. | (2,$\sqrt{6}$) | D. | (1,$\sqrt{7}$) |
7.设$\overrightarrow a=(2,-1),向量\overrightarrow b满足2\overrightarrow a-\overrightarrow b$=(-1,3),则$\overrightarrow b$等于( )
| A. | (-5,5) | B. | (5,-5) | C. | (-3,3) | D. | (3,-3) |
17.函数y=sin(2x+$\frac{π}{12}$)的图象经过平移后所得图象关于点($\frac{π}{12}$,0)中心对称,这个平移变换可以是( )
| A. | 向左平移$\frac{π}{8}$个单位 | B. | 向左平移$\frac{π}{4}$个单位 | ||
| C. | 向右平移$\frac{π}{8}$个单位 | D. | 向右平移$\frac{π}{4}$个单位 |
9.某几何体的三视图如图所示,则该几何体的表面积是( )
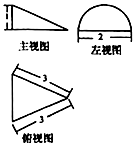

| A. | $\frac{\sqrt{2}}{3}$π | B. | 2$\sqrt{2}$+2π | C. | $\frac{2\sqrt{2}}{3}$π | D. | 2$\sqrt{2}$+$\frac{3}{2}$π |
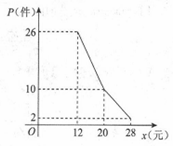 某网店经营的一种商品进价是每件10元,根据一周的销售数据得出周销量P(件)与单价x(元)之间的关系如图折线所示,该网店与这种商品有关的周开支均为25元.
某网店经营的一种商品进价是每件10元,根据一周的销售数据得出周销量P(件)与单价x(元)之间的关系如图折线所示,该网店与这种商品有关的周开支均为25元.