题目内容
7.某车间加工零件的数量x与加工时间y的统计数据如表:| 零件数x(个) | 18 | 20 | 22 |
| 加工时间y(分钟) | 27 | 30 | 33 |
分析 求出样本数据的中心坐标($\overline{x}$,$\overline{y}$),代入回归直线方程,求出$\widehat{a}$,得到回归直线方程,然后求解加工100个零件所需要的加工时间.
解答 解:由题意得:$\overline{x}$=$\frac{1}{3}$(18+20+22)=20,$\overline{y}$=$\frac{1}{3}$(27+30+33)=30,
故$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$=30-0.9×20=12,
故$\widehat{y}$=0.9x+12,x=100时:$\widehat{y}$=102,
故答案为:102.
点评 本题考查线性回归方程的求法和应用,解题的关键是正确应用最小二乘法求出线性回归方程的系数的运算,再一点就是代入样本中心点可以求出字母a的值,是一个中档题目.

练习册系列答案
相关题目
15.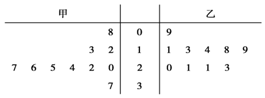 某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个.命中个数的茎叶图如图,则下面结论中错误的一个是( )
某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个.命中个数的茎叶图如图,则下面结论中错误的一个是( )
 某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个.命中个数的茎叶图如图,则下面结论中错误的一个是( )
某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个.命中个数的茎叶图如图,则下面结论中错误的一个是( )| A. | 乙的众数是21 | B. | 甲的中位数是24 | ||
| C. | 甲的极差是29 | D. | 甲罚球命中率比乙高 |
2.下列说法正确的是( )
| A. | 在频率分布直方图中,众数左边和右边的直方图的面积相等 | |
| B. | 为调查高三年级的240名学生完成作业所需的时间,由教务处对高三年级的学生进行编号,从001到240抽取学号最后一位为3的学生进行调查,则这种抽样方法为分层抽样 | |
| C. | “x≠1”是“x2-3x+2≠0”的充分不必要条件 | |
| D. | 命题p:“?x0∈R,${x_0}^2-3{x_0}+2<0$”的否定为:“?x∈R,x2-3x+2≥0” |
12.某连锁经营公司所属5个零售店某月的销售额和利润额资料如下表:
(Ⅰ)用最小二乘法计算利润额y对销售额x的回归直线方程$\widehaty=\widehatbx+\widehata$;
(Ⅱ)当销售额为4(千万元)时,估计利润额的大小.
附:线性回归方程$\widehaty=\widehatbx+\widehata$中,$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}}$,$\widehata=\overline y-\widehatb\overline x$.
| 商店名称 | A | B | C | D | E |
| 销售额x(千万元) | 3 | 5 | 6 | 7 | 9 |
| 利润额y(千万元) | 2 | 3 | 3 | 4 | 5 |
(Ⅱ)当销售额为4(千万元)时,估计利润额的大小.
附:线性回归方程$\widehaty=\widehatbx+\widehata$中,$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}}$,$\widehata=\overline y-\widehatb\overline x$.
16.已知幂函数y=f(x)的图象过点(2,4),则log2f($\frac{1}{2}$)=( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 2 | D. | -2 |
17.函数y=sin(2x+$\frac{π}{12}$)的图象经过平移后所得图象关于点($\frac{π}{12}$,0)中心对称,这个平移变换可以是( )
| A. | 向左平移$\frac{π}{8}$个单位 | B. | 向左平移$\frac{π}{4}$个单位 | ||
| C. | 向右平移$\frac{π}{8}$个单位 | D. | 向右平移$\frac{π}{4}$个单位 |
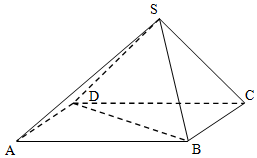 如图所示,在四棱锥S-ABCD中,底面ABCD是矩形,侧面SDC⊥底面ABCD,且AB=2,SC=SD=$\sqrt{2}$.
如图所示,在四棱锥S-ABCD中,底面ABCD是矩形,侧面SDC⊥底面ABCD,且AB=2,SC=SD=$\sqrt{2}$.