题目内容
8.直线x-y-1=0的倾斜角与其在y轴上的截距分别是( )| A. | 135°,1 | B. | 45°,-1 | C. | 45°,1 | D. | 135°,-1 |
分析 根据题意,将直线的方程变形为斜截式方程,可得直线的斜率与其在y轴上的截距,利用倾斜角与斜率的关系,可得其倾斜角,即可得答案.
解答 解:根据题意,直线的方程为x-y-1=0,变形可得y=x-1,
则其斜率k=1,倾斜角θ=45°,
在y轴上的截距为-1;
故选:B.
点评 本题考查直线的一般式方程的应用,要根据题意,将直线的方程变形为斜截式方程.

练习册系列答案
相关题目
16.已知幂函数y=f(x)的图象过点(2,4),则log2f($\frac{1}{2}$)=( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 2 | D. | -2 |
20.设直线l与椭圆$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{8}=1$相交于A,B两点,与圆(x-1)2+y2=r2(r>0)相切于点M,且M为线段AB的中点,若这样的直线l恰有4条,则r的取值范围是( )
| A. | (1,$\sqrt{6}$) | B. | (2,$\sqrt{7}$) | C. | (2,$\sqrt{6}$) | D. | (1,$\sqrt{7}$) |
17.函数y=sin(2x+$\frac{π}{12}$)的图象经过平移后所得图象关于点($\frac{π}{12}$,0)中心对称,这个平移变换可以是( )
| A. | 向左平移$\frac{π}{8}$个单位 | B. | 向左平移$\frac{π}{4}$个单位 | ||
| C. | 向右平移$\frac{π}{8}$个单位 | D. | 向右平移$\frac{π}{4}$个单位 |
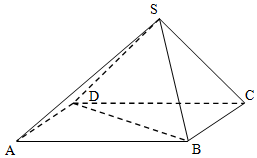 如图所示,在四棱锥S-ABCD中,底面ABCD是矩形,侧面SDC⊥底面ABCD,且AB=2,SC=SD=$\sqrt{2}$.
如图所示,在四棱锥S-ABCD中,底面ABCD是矩形,侧面SDC⊥底面ABCD,且AB=2,SC=SD=$\sqrt{2}$.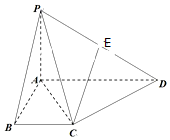 如图,在四棱锥P-ABCD中,已知PA⊥平面ABCD,∠BAD=90°,AD∥BC,PA=AB=BC=1,AD=2,E为PD的中点.
如图,在四棱锥P-ABCD中,已知PA⊥平面ABCD,∠BAD=90°,AD∥BC,PA=AB=BC=1,AD=2,E为PD的中点.