题目内容
已知椭圆C:
+
=1(a>b>0)过点Q(-1,
),且离心率e=
.
(1)求椭圆C的方程;
(2)设直线l:y=kx+1与曲线C交于M、N两点,当线段MN的中点在直线x+2y=1上时,求直线l的方程.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| ||
| 2 |
(1)求椭圆C的方程;
(2)设直线l:y=kx+1与曲线C交于M、N两点,当线段MN的中点在直线x+2y=1上时,求直线l的方程.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由已知条件得
,由此能求出椭圆C的方程.
(2)设M(x1,y1),N(x2,y2),MN的中点(x0,y0),利用点差法能求出直线l的方程.
|
(2)设M(x1,y1),N(x2,y2),MN的中点(x0,y0),利用点差法能求出直线l的方程.
解答:
解:(Ⅰ)∵椭圆C:
+
=1(a>b>0)过点Q(-1,
),且离心率e=
,
∴
,解得
,
∴椭圆C的方程为
+y2=1.
(2)设M(x1,y1),N(x2,y2),MN的中点(x0,y0)
得
,
两式相减,得 (
-
)+2(
-
)=0(x1+x2)+2(y1+y2)•(
)=0(x1≠x2),
即x0+2y0•k=0,又x0+2y0=0,∴k=1,
∴直线l的方程为y=x+1.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| ||
| 2 |
∴
|
|
∴椭圆C的方程为
| x2 |
| 2 |
(2)设M(x1,y1),N(x2,y2),MN的中点(x0,y0)
得
|
两式相减,得 (
| x | 2 1 |
| x | 2 2 |
| y | 2 1 |
| y | 2 2 |
| y1-y2 |
| x1-x2 |
即x0+2y0•k=0,又x0+2y0=0,∴k=1,
∴直线l的方程为y=x+1.
点评:本题考查椭圆方程的求法,考查直线方程的求法,解题时要认真审题,注意点差法的合理运用.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
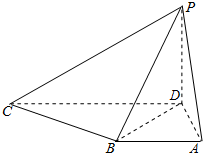 在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是直角梯形,AB∥CD,∠BAD=90°,AB=AD=1,PD=
在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是直角梯形,AB∥CD,∠BAD=90°,AB=AD=1,PD=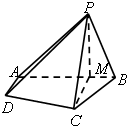 在四棱锥P-ABCD中,AD∥BC,∠ABC=∠APB=90°,点M是线段AB上的一点,且PM⊥CD,AB=BC=2PB=2AD=4BM.
在四棱锥P-ABCD中,AD∥BC,∠ABC=∠APB=90°,点M是线段AB上的一点,且PM⊥CD,AB=BC=2PB=2AD=4BM.