题目内容

已知命题P：ln（x-2）＜0，Q：（x-a）（x-3a＜0），（a＞0），若命题P是 Q 的充分不必要条件，求a的取值范围．
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：根据不等式的性质求出P，Q对应的等价条件，利用充分条件和必要条件的定义建立条件关系即可得到结论．
解答： 解：由ln（x-2）＜0，得0＜x-2＜1，即2＜x＜3，即P：2＜x＜3，
由（x-a）•（x-3a）＜0，得a＜x＜3a，即Q：a＜x＜3a，
若P是 Q 的充分不必要条件，
则
a≤2
3a≥3
，即
a≤2
a≥1
，
则1≤a≤2，
即实数a的取值范围是[1，2]．
点评：本题主要考查充分条件和必要条件的应用，求出命题的等价条件是解决本题的关键．
练习册系列答案
相关题目
已知过曲线C上任意一点P作直线x=-2p（p＞0）的垂线，垂足为M，且OP⊥OM．
（1）求曲线C的方程；
（2）设A、B是曲线C上两个不同点，直线OA和OB的倾斜角分别为α和β，当α，β变化且α+β为定值θ（0＜θ＜π）时，证明直线AB恒过定点，并求出该定点的坐标．
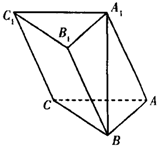如图，在三棱柱ABC-A1B1C1中，A1B⊥平面ABC，AB⊥AC．
（1）求证：AC⊥BB1；
（2）若AB=AC=A1B=2，在棱B1C1上确定一点P，使二面角P-AB-A1的平面角的余弦值为
2
5
5
．
计算：
x
x
+x
y
xy-y2
-
x+
xy
+y
x
x
-y
y
．
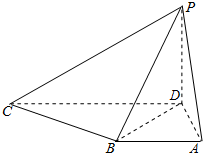在四棱锥P-ABCD中，PD⊥底面ABCD，底面ABCD是直角梯形，AB∥CD，∠BAD=90°，AB=AD=1，PD=
3
，CD=2．
（Ⅰ）求证：BC⊥平面PBD；
（Ⅱ）点E是线段PC上的一个动点，二面角E-BA-D的大小是否可以为30°？若可以，求出线段PE的长．
作出函数y=
1
x
，(0＜x＜1)
x，(x≥1)
的图象，并求其值域．
已知an+1=
an-6
an+6
，a1=2，求an．
已知椭圆E：
x2
a2
+
y2
b2
=1（a＞b＞0）的离心率为
2
2
，直线l分别经过椭圆长轴和短轴的一个顶点，且与圆C：x2+y2=
2
3
相切，
（Ⅰ）求椭圆E的方程；
（Ⅱ）P为圆C上任意一点，以P为切点作圆C的切线与椭圆E相交于点M，N，求线段|MN|的取值范围．
设F1、F2分别是椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的左、右焦点，点P在椭圆C上，线段PF1的中点在y轴上，若∠PF1F2=30°，则椭圆C的离心率为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网