题目内容
 “交通指数”是反映道路网畅通或拥堵的概念性指数值.交通指数的取值范围为0至10,分为5个等级:其中[0,2)为畅通,[2,4)为基本畅通,[4,6)为轻度拥堵,[6,8)为中度拥堵,[8,10]为严重拥堵.晚高峰时段,某市交通指挥中心选取了市区60个交通路段,依据其交通指数数据绘制的频数分布表及频率分布直方图如图所示:
“交通指数”是反映道路网畅通或拥堵的概念性指数值.交通指数的取值范围为0至10,分为5个等级:其中[0,2)为畅通,[2,4)为基本畅通,[4,6)为轻度拥堵,[6,8)为中度拥堵,[8,10]为严重拥堵.晚高峰时段,某市交通指挥中心选取了市区60个交通路段,依据其交通指数数据绘制的频数分布表及频率分布直方图如图所示:| 交通指数 | 频数 | 频率 |
| [0,2) | m1 | n1 |
| [2,4) | m2 | n2 |
| [4,6) | 15 | 0.25 |
| [6,8) | 18 | 0.3 |
| [8,10] | 12 | 0.2 |
(Ⅱ)用分层抽样的方法从交通指数在[0,2)和[2,4)的路段中抽取一个容量为5的样本,将该样本看成一个总体,从中随机抽出2个路段,求至少有一个路段为畅通的概率.
考点:古典概型及其概率计算公式,频率分布直方图
专题:概率与统计
分析:(Ⅰ) 根据频率分布直方图,求出值即可.
(Ⅱ)列举出所有的基本事件,然后找到满足条件的基本事件,根据古典概率公式计算即可.
(Ⅱ)列举出所有的基本事件,然后找到满足条件的基本事件,根据古典概率公式计算即可.
解答:
解:(I)由频率分布直方图,得交通指数在[2,4)的频率为
1-(0.05+0.1+0.125+0.15)×2=0.15.
所以,n1=0.05×2=0.1,m1=0.1×60=6,
n2=0.15,m2=0.15×60=9,
频率分布直方图为:

(II)依题意知,取出的5个路段中,交通指数在[0,2)内的有2个,设为啊,b,
交通指数在[2,4)内的有3个,设为想,x,y,z,
则交通指数在[0,4)的基本事件空间为
Ω={ab,ax,ay,az,bx,by,bz,xy,xz,yz},基本事件总数为10,
事件A=“至少有一个路段为畅通”,
则A={ab,ax,ay,az,bx,by,bz},基本事件总数为7.
P(A)=
,
所以至少有一个路段为畅通的概率为
.
1-(0.05+0.1+0.125+0.15)×2=0.15.
所以,n1=0.05×2=0.1,m1=0.1×60=6,
n2=0.15,m2=0.15×60=9,
频率分布直方图为:

(II)依题意知,取出的5个路段中,交通指数在[0,2)内的有2个,设为啊,b,
交通指数在[2,4)内的有3个,设为想,x,y,z,
则交通指数在[0,4)的基本事件空间为
Ω={ab,ax,ay,az,bx,by,bz,xy,xz,yz},基本事件总数为10,
事件A=“至少有一个路段为畅通”,
则A={ab,ax,ay,az,bx,by,bz},基本事件总数为7.
P(A)=
| 7 |
| 10 |
所以至少有一个路段为畅通的概率为
| 7 |
| 10 |
点评:本题主要考查频率分布直方图和概率的计算公式,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
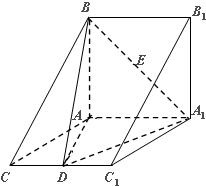 如图在三棱柱ABC-A1B1C1中,平面ABB1A1⊥平面AA1C1C,∠BAA1=90°,∠CAA1=120°,AB=AC=AA1=2,D是棱CC1的中心点.
如图在三棱柱ABC-A1B1C1中,平面ABB1A1⊥平面AA1C1C,∠BAA1=90°,∠CAA1=120°,AB=AC=AA1=2,D是棱CC1的中心点.

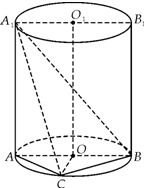 如图,已知AB是圆柱OO1底面圆O的直径,底面半径R=1,圆柱的表面积为8π;点C在底面圆O上,且∠AOC=120°.
如图,已知AB是圆柱OO1底面圆O的直径,底面半径R=1,圆柱的表面积为8π;点C在底面圆O上,且∠AOC=120°.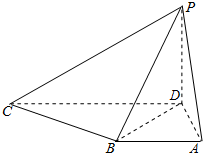 在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是直角梯形,AB∥CD,∠BAD=90°,AB=AD=1,PD=
在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是直角梯形,AB∥CD,∠BAD=90°,AB=AD=1,PD=