题目内容
设函数f(x)是定义在R上的偶函数,且对任意的x∈R恒有f(x+1)=f(1-x),已知当x∈[0,1]时,f(x)=(
)1-x,则:
①f(x+2)=f(x);
②函数f(x)在(1,2)上递减,在(2,3)上递增;
③函数f(x)的最大值是1,最小值是0;
④当x∈(3,4)时,f(x)=(
)x-3.
其中正确结论的个数是( )
| 1 |
| 2 |
①f(x+2)=f(x);
②函数f(x)在(1,2)上递减,在(2,3)上递增;
③函数f(x)的最大值是1,最小值是0;
④当x∈(3,4)时,f(x)=(
| 1 |
| 2 |
其中正确结论的个数是( )
| A、1 | B、2 | C、3 | D、4 |
考点:奇偶性与单调性的综合
专题:函数的性质及应用
分析:根据条件得到函数的周期为2,利用函数的单调性奇偶性,周期性的之间的关系分别进行判断即可.
解答:
解:∵函数f(x)是定义在R上的偶函数,且f(x+1)=f(1-x),
∴f(x+1)=f(1-x)=f(x-1),
即f(x+2)=f(x),故①正确.
由f(x+2)=f(x)得函数的周期是2,
∵当x∈[0,1]时,f(x)=(
)1-x=2x-1为增函数,
∴函数在[-1,0]上为减函数,在(1,2)上递减,在(2,3)上递增,故②正确.
∵当x∈[0,1]时,f(x)=(
)1-x=2x-1为增函数,∴当x∈[0,1]时,f(x)的最大值为f(1)=1,最小值为f(0)=
.故③错误.
∵x∈(-1,0)时,-x∈(0,1),则f(x)=f(-x)=2-x-1=(
)x+1,
当x∈(3,4)时,x-4∈(-1,0),则f(x)=f(x-4)=(
)x-4+1=(
)x-3,故④正确.
其中正确的是①②④,
故选:C
∴f(x+1)=f(1-x)=f(x-1),
即f(x+2)=f(x),故①正确.
由f(x+2)=f(x)得函数的周期是2,
∵当x∈[0,1]时,f(x)=(
| 1 |
| 2 |
∴函数在[-1,0]上为减函数,在(1,2)上递减,在(2,3)上递增,故②正确.
∵当x∈[0,1]时,f(x)=(
| 1 |
| 2 |
| 1 |
| 2 |
∵x∈(-1,0)时,-x∈(0,1),则f(x)=f(-x)=2-x-1=(
| 1 |
| 2 |
当x∈(3,4)时,x-4∈(-1,0),则f(x)=f(x-4)=(
| 1 |
| 2 |
| 1 |
| 2 |
其中正确的是①②④,
故选:C
点评:本题主要考查命题的真假判断,根据条件得到函数的周期性是解决本题的关键.综合考查函数的性质的综合应用.

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目

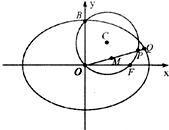 已知圆C经(x-1)2+(y-2)2=5经过椭圆E:
已知圆C经(x-1)2+(y-2)2=5经过椭圆E: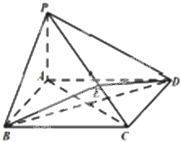 如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE.PA=1,AD=2.
如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE.PA=1,AD=2.