题目内容
已知a1=1,且an+1=2nan,求an.
考点:数列的概念及简单表示法
专题:点列、递归数列与数学归纳法
分析:由an+1=2nan,得
=2n,利用累乘法可求得an.
| an+1 |
| an |
解答:
解:由an+1=2nan,得
=2n,
∴n≥2时,
=2n-1,
∴n≥2时,an=a1•
•
…
=1×2×22×…×2n-1
=21+2+…+(n-1)
=2
,
又a1=1适合上式,
∴an=2
.
| an+1 |
| an |
∴n≥2时,
| an |
| an-1 |
∴n≥2时,an=a1•
| a2 |
| a1 |
| a3 |
| a2 |
| an |
| an-1 |
=21+2+…+(n-1)
=2
| n(n-1) |
| 2 |
又a1=1适合上式,
∴an=2
| n(n-1) |
| 2 |
点评:本题考查由数列递推式求数列通项,属中档题,若已知
=f(n)求数列通项,常用累乘法求解,注意检验n=1时的情形.
| an+1 |
| an |

练习册系列答案
相关题目
记数列{an}的前n项和为Sn,若不等式an2+
≥ma12对任意等差数列{an}及任意正整数n都成立,则实数m的最大值为( )
| Sn2 |
| n2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
设定义域为R的函数f(x)满足f(x+1)=
+
,且f(-1)=
,则f(2014)的值为( )
| 1 |
| 2 |
| f(x)-[f(x)]2 |
| 1 |
| 2 |
| A、-1 | ||
| B、1 | ||
| C、2014 | ||
D、
|
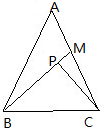 如图,在△ABC中,AB=AC=3
如图,在△ABC中,AB=AC=3