题目内容
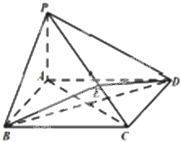 如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE.PA=1,AD=2.
如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE.PA=1,AD=2.(1)证明:BD⊥平面PAC;
(2)求二面角B-PC-A的正切值.
考点:用空间向量求平面间的夹角,直线与平面垂直的判定
专题:空间角
分析:(1)由PC⊥平面BDE,得到PC⊥BD,再由PA⊥平面ABCD得到PA⊥BD,然后由线面垂直的判断得答案;
(2)设AC与BD交于点O,连接OE,可得∠OEB就是二面角B-PC-A的平面角,然后利用△OEB∽△PAC及解直角三角形求得二面角B-PC-A的正切值.
(2)设AC与BD交于点O,连接OE,可得∠OEB就是二面角B-PC-A的平面角,然后利用△OEB∽△PAC及解直角三角形求得二面角B-PC-A的正切值.
解答:
解:(1)证明:如图,
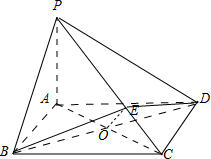
∵PC⊥平面BDE,BD?平面BDE,
∴PC⊥BD,
又∵PA⊥平面ABCD,BD?平面ABCD,
∴PA⊥BD,
而PC∩PA=P,PC?平面PAC,PA?平面PAC,
∴BD⊥平面PAC;
(2)设AC与BD交于点O,连接OE
∵PC⊥平面BDE,OE?平面BDE,BE?平面BDE,
∴PC⊥OE,PC⊥BE,
于是∠OEB就是二面角B-PC-A的平面角,
又∵BD⊥平面PAC,OE?平面PAC,
∴△OEB是直角三角形.
由△OEB∽△PAC,可得
=
,
而AB=AD=2,
∴AC=2
,OC=
,
而PA=1,
∴PC=3,
于是OE=
×OC=
×
=
,而OB=
,
于是二面角B-PC-A的正切值为
=3.

∵PC⊥平面BDE,BD?平面BDE,
∴PC⊥BD,
又∵PA⊥平面ABCD,BD?平面ABCD,
∴PA⊥BD,
而PC∩PA=P,PC?平面PAC,PA?平面PAC,
∴BD⊥平面PAC;
(2)设AC与BD交于点O,连接OE
∵PC⊥平面BDE,OE?平面BDE,BE?平面BDE,
∴PC⊥OE,PC⊥BE,
于是∠OEB就是二面角B-PC-A的平面角,
又∵BD⊥平面PAC,OE?平面PAC,
∴△OEB是直角三角形.
由△OEB∽△PAC,可得
| OE |
| OC |
| PA |
| PC |
而AB=AD=2,
∴AC=2
| 2 |
| 2 |
而PA=1,
∴PC=3,
于是OE=
| PA |
| PC |
| 1 |
| 3 |
| 2 |
| ||
| 3 |
| 2 |
于是二面角B-PC-A的正切值为
| OB |
| OE |
点评:本题考查了直线与平面垂直的判断,考查了二面角的平面角的找法与求解,解答此题的关键在于找到二面角的平面角,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设定义域为R的函数f(x)满足f(x+1)=
+
,且f(-1)=
,则f(2014)的值为( )
| 1 |
| 2 |
| f(x)-[f(x)]2 |
| 1 |
| 2 |
| A、-1 | ||
| B、1 | ||
| C、2014 | ||
D、
|