题目内容
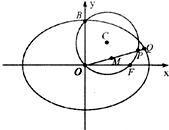已知圆C经（x-1）2+（y-2）2=5经过椭圆E：| x2 |
| a2 |
| y2 |
| b2 |
（1）求椭圆E的方程；
（2）过原点O的射线l在第一象限与椭圆E的交点为Q，与圆C的交点为P，M为OP的中点，求
| OM |
| OQ |
考点：直线与圆锥曲线的关系,椭圆的标准方程
专题：计算题,直线与圆,圆锥曲线的定义、性质与方程
分析：（1）在圆（x-1）2+（y-2）2=5中，令y=0，得F（2，0），令x=0，得B（0，4），由此能求出椭圆方程；
（2）设点Q（x0，y0），x0＞0，y0＞0，由于M为OP的中点，则CM⊥OQ，则
•
=（
+
）•
=
•
=（1，2）•（x0，y0）=x0+2y0，设t=x0+2y0，与
+
=1联立，消去x0，再由判别式为0，即可得到最大值．
（2）设点Q（x0，y0），x0＞0，y0＞0，由于M为OP的中点，则CM⊥OQ，则
| OM |
| OQ |
| OC |
| CM |
| OQ |
| OC |
| OQ |
| x02 |
| 20 |
| y02 |
| 16 |
解答：
解：（1）在圆C：（x-1）2+（y-2）2=5中，
令y=0，得F（2，0），即c=2，
令x=0，得B（0，4），即b=4，
∴a2=b2+c2=20，
∴椭圆E的方程为：
+
=1．
（2）设点Q（x0，y0），x0＞0，y0＞0，
由于M为OP的中点，则CM⊥OQ，
则
•
=（
+
）•
=
•
=（1，2）•（x0，y0）
=x0+2y0，
又
+
=1，
设t=x0+2y0，与
+
=1联立，得：21y02-16ty0+4t2-80=0，
令△=0，得256t2-84（4t2-80）=0，
解得t=±2
．
又点Q（x0，y0）在第一象限，
∴当y0=
时，
•
取最大值2
．
令y=0，得F（2，0），即c=2，
令x=0，得B（0，4），即b=4，
∴a2=b2+c2=20，
∴椭圆E的方程为：
| x2 |
| 20 |
| y2 |
| 16 |
（2）设点Q（x0，y0），x0＞0，y0＞0，
由于M为OP的中点，则CM⊥OQ，
则
| OM |
| OQ |
| OC |
| CM |
| OQ |
| OC |
| OQ |
=（1，2）•（x0，y0）
=x0+2y0，
又
| x02 |
| 20 |
| y02 |
| 16 |
设t=x0+2y0，与
| x02 |
| 20 |
| y02 |
| 16 |
令△=0，得256t2-84（4t2-80）=0，
解得t=±2
| 21 |
又点Q（x0，y0）在第一象限，
∴当y0=
16
| ||
| 21 |
| OM |
| OQ |
| 21 |
点评：本题考查直线、圆、椭圆、平面向量等基础知识，考查直线与圆锥曲线的位置关系，考查运算求解能力、推理论证能力，考查数形结合、化归转化及函数与方程等数学思想．
练习册系列答案
名师导航单元期末冲刺100分系列答案
名校名卷单元同步训练测试题系列答案
相关题目
设定义域为R的函数f（x）满足f（x+1）=
+
，且f（-1）=
，则f（2014）的值为（ ）
| 1 |
| 2 |
| f(x)-[f(x)]2 |
| 1 |
| 2 |
| A、-1 | ||
| B、1 | ||
| C、2014 | ||
D、
|