题目内容
19.已知O为坐标原点,A,B,C三点的坐标分别是(2,-1,2),(4,5,-1),(-2,2,3),求点P坐标.使:(1)$\overrightarrow{OP}$=$\frac{1}{2}$($\overrightarrow{AB}$-$\overrightarrow{AC}$);
(2)$\overrightarrow{AP}$=$\frac{1}{2}$($\overrightarrow{AB}$-$\overrightarrow{AC}$)
分析 (1)设出点P的坐标,利用向量的坐标运算求出向量$\overrightarrow{OP}$,即得点P的坐标;
(2)由(1)的运算,再求出向量$\overrightarrow{OP}$的坐标表示,即可得出点P的坐标;
解答 解:(1)设点P(x,y,z),∵$\overrightarrow{AB}$=(2,6,-3),$\overrightarrow{AC}$=(-4,3,1),
∴$\overrightarrow{OP}$=$\frac{1}{2}$($\overrightarrow{AB}$-$\overrightarrow{AC}$)=$\frac{1}{2}$(6,3,-4)=(3,$\frac{3}{2}$,-2),
∴点P的坐标为(3,$\frac{3}{2}$,-2);
(2)由(1)知,$\overrightarrow{AP}$=$\frac{1}{2}$($\overrightarrow{AB}$-$\overrightarrow{AC}$)=(3,$\frac{3}{2}$,-2),
∴$\overrightarrow{OP}$-$\overrightarrow{OA}$=(3,$\frac{3}{2}$,-2),
∴$\overrightarrow{OP}$=(3,$\frac{3}{2}$,-2)+(2,-1,2)=(5,$\frac{1}{2}$,0),
∴点P的坐标为(5,-$\frac{1}{2}$,0).
点评 本题考查了空间向量的坐标表示与运算的应用问题,是基础题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.已知f(x)=$\left\{\begin{array}{l}{x+1,x≤0}\\{lo{g}_{2}x,x>0}\end{array}\right.$,若函数y=f[f(x)]-m存在三个零点,则实数m的取值范围是( )
| A. | [0,1] | B. | (0,1] | C. | (-∞,0] | D. | (-∞,0) |
7.已知$\overrightarrow{a}$=(-2,1,3),$\overrightarrow{b}$=(-1,2,1),若$\overrightarrow{a}$⊥($\overrightarrow{a}$-λ$\overrightarrow{b}$),则实数λ的值为( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | -$\frac{1}{2}$ | D. | -2 |
4.若实数x,y满足不等式组$\left\{\begin{array}{l}{2x+y≤4}\\{x≥0}\\{y≥0}\end{array}\right.$,则$\frac{y+1}{2x+2}$的取值范围是( )
| A. | [$\frac{1}{6}$,$\frac{5}{2}$] | B. | [$\frac{1}{3}$,5] | C. | [$\frac{2}{3}$,10] | D. | [-$\frac{1}{3}$,5] |
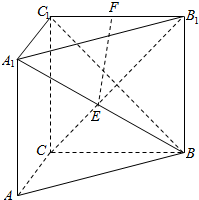 如图,三棱柱CB=AC=CC1,CB⊥AC,E,F分别是A1B,B1C1的中点,AA1⊥底面ABC.
如图,三棱柱CB=AC=CC1,CB⊥AC,E,F分别是A1B,B1C1的中点,AA1⊥底面ABC.