题目内容
8.已知函数y=a-bcos(2x+$\frac{π}{6}$)的最大值为3,最小值为-1.(1)求a,b的值;
(2)设函数g(x)=4asin(bx-$\frac{π}{3}$),求方程g(x)-2=0在区间[$\frac{π}{6}$,$\frac{5}{6}$π]上所有根之和.
分析 (1)由条件利用函数的最大值为a+|b|=3,最小值为a-|b|=-1,求得a、b的值.
(2)本题即求函数y=4sin(bx-$\frac{π}{3}$)的图象和直线y=2的交点的横坐标之和,数形结合可得结论.
解答 解:(1)由于函数y=a-bcos(2x+$\frac{π}{6}$)的最大值为a+|b|=3,最小值为a-|b|=-1,
求得a=1,|b|=2,∴a=1,b=2; 或a=1,b=-2.
(2)设函数g(x)=4sin(bx-$\frac{π}{3}$),方程g(x)-2=0在区间[$\frac{π}{6}$,$\frac{5}{6}$π]上所有根之和,
即函数y=4sin(bx-$\frac{π}{3}$)的图象和直线y=2的交点的横坐标之和.
当b=2时,令t=2x-$\frac{π}{3}$∈[0,$\frac{4π}{3}$],x=$\frac{t}{2}$+$\frac{π}{6}$,本题即求y=4sint的图象和直线y=2的交点的横坐标之和.
如图所示,
∵t1+t2=π,∴x1+x2=$\frac{5π}{6}$.
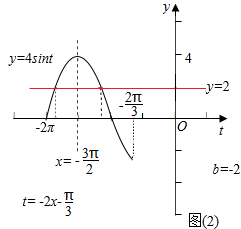
当b=-2时,令t=-2x-$\frac{π}{3}$∈[-2π,-$\frac{2π}{3}$],x=-$\frac{t}{2}$-$\frac{π}{6}$,本题即求y=4sint的图象和直线y=2的交点的横坐标之和.
如图所示,
∵t1+t2=-3π,∴x1+x2=$\frac{3π}{2}$-$\frac{π}{3}$=$\frac{7π}{6}$.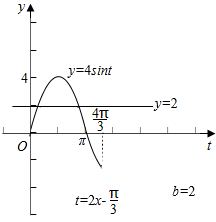
点评 本题主要考查正弦函数的最值,函数的零点与方程的根的关系,体现了转化、数形结合的数学思想,属于中档题.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
20.下列命题中正确的是( )
| A. | 垂直于同一直线的两直线平行 | |
| B. | 平行于同一平面的两直线平行 | |
| C. | 平行于同一直线的两直线平行 | |
| D. | 与同一平面所成的角相等的两直线平行 |