题目内容
11.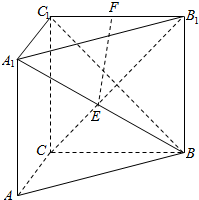 如图,三棱柱CB=AC=CC1,CB⊥AC,E,F分别是A1B,B1C1的中点,AA1⊥底面ABC.
如图,三棱柱CB=AC=CC1,CB⊥AC,E,F分别是A1B,B1C1的中点,AA1⊥底面ABC.(1)求证:B1C⊥平面A1BC1;
(2)求证:EF∥平面ACC1A1.
分析 (1)以A为原点建立空间直角坐标系C-xyz,利用向量法能证明B1C⊥BC1,B1C⊥BA1,即可证明B1C⊥平面A1BC1.
(2)由(1)可得:$\overrightarrow{EF}$=(0,-1,1),平面ACC1A1的法向量为$\overrightarrow{n}$=(1,0,0),利用$\overrightarrow{EF}$•$\overrightarrow{n}$=0,即可证明EF∥平面ACC1A1.
解答  证明:(1)如图,以C为原点,CB,CA,CC1为x,y,z轴正方向建立空间直角坐标系A-xyz,
证明:(1)如图,以C为原点,CB,CA,CC1为x,y,z轴正方向建立空间直角坐标系A-xyz,
设AC=2,则由CB=AC=CC1,得C(0,0,0),B(2,0,0),C1(0,0,2),A1(0,2,2),B1(2,0,2),(6分)
因为E,F分别是A1B,B1C1的中点,
所以E(1,1,1),F(1,0,2).(7分)
所以$\overrightarrow{{B}_{1}C}$=(-2,0,-2),$\overrightarrow{B{C}_{1}}$=(-2,0,2),$\overrightarrow{B{A}_{1}}$=(-2,2,2),
因为:$\overrightarrow{{B}_{1}C}$•$\overrightarrow{B{C}_{1}}$=(-2,0,-2)•(-2,0,2)=0,
所以:B1C⊥BC1,
因为:$\overrightarrow{{B}_{1}C}$•$\overrightarrow{B{A}_{1}}$=(-2,0,-2)•(-2,2,2)=0,
所以:B1C⊥BA1,
又A1B∩C1B=B,
所以B1C⊥平面A1BC1.(9分)
(2)由(1)可得:$\overrightarrow{EF}$=(0,-1,1),
由题意可得平面ACC1A1的法向量为$\overrightarrow{n}$=(1,0,0),
可得:$\overrightarrow{EF}$•$\overrightarrow{n}$=(0,-1,1)•(1,0,0)=0,
可得:EF∥平面ACC1A1.
点评 本题主要考查了直线与平面垂直的判定,直线与平面平行的判定,考查了空间想象能力和推理论证能力,解题时要认真审题,注意向量法的合理运用.

 阅读快车系列答案
阅读快车系列答案| A. | 垂直于同一直线的两直线平行 | |
| B. | 平行于同一平面的两直线平行 | |
| C. | 平行于同一直线的两直线平行 | |
| D. | 与同一平面所成的角相等的两直线平行 |
| A. | (1,0) | B. | (2,1) | C. | 2 | D. | 1 |