题目内容
△ABC中，下面四个等式中不正确的是（ ）
| A、cos（A+B）=-cosC | ||||
| B、sin2（A+B）=sin2C | ||||
C、tan
| ||||
D、cos3（A+B）=1-2cos2
|
考点：三角函数恒等式的证明
专题：三角函数的求值
分析：由条件利用三角恒等变换化简所给等式的左边，可得结果，从而得出结论．
解答：
解：△ABC中，∵A+B+C=π，利用诱导公式可得cos（A+B）=-cosC，故A正确．
由于sin2（A+B）=sin2（π-C）=sin（2π-2C）=-sin2C，故B不正确．
由于tan
=tan
=cot
，故C正确．
由于cos3（A+B）=cos3（π-C）=cos（3π-3C）=-cos3C=1-2cos2
，
故选：B．
由于sin2（A+B）=sin2（π-C）=sin（2π-2C）=-sin2C，故B不正确．
由于tan
| A+B |
| 2 |
| π-C |
| 2 |
| C |
| 2 |
由于cos3（A+B）=cos3（π-C）=cos（3π-3C）=-cos3C=1-2cos2
| C |
| 3 |
故选：B．
点评：本题主要考查三角函数的恒等变换及化简求值，属于基础题．
练习册系列答案
相关题目
已知函数f（x）=-x+log2
+1，则f（
）+f（-
）的值为（ ）
| 1-x |
| 1+x |
| 1 |
| 2 |
| 1 |
| 2 |
| A、2 | ||
| B、-2 | ||
| C、0 | ||
D、2log2
|
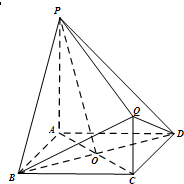如图，PA，QC都与正方形ABCD所在平面垂直，AB=PA=2QC=2，AC∩BD=O
