题目内容
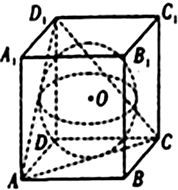 如图,已知球O是棱长为1的正方体ABCD-A1B1C1D1的内切球,则以B1为顶点,以球被平面ACD1截得的圆为底面的圆锥的全面积为
如图,已知球O是棱长为1的正方体ABCD-A1B1C1D1的内切球,则以B1为顶点,以球被平面ACD1截得的圆为底面的圆锥的全面积为考点:旋转体(圆柱、圆锥、圆台)
专题:空间位置关系与距离
分析:根据正方体和球的结构特征,求得球O被平面ACD1所截得的圆的半径r,再通过利用球的性质求出O到平面ACD1的距离d,进而求出圆锥的高,再由勾股定理求出圆锥的母线,最后利用圆锥的表面积求解即可.
解答:
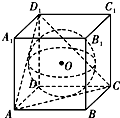 解:如图,O为球心,也是正方体的中心,
解:如图,O为球心,也是正方体的中心,
设球O被平面ACD1所截得的圆的半径为r,AC中点为M,
则r=
D1M=
,
球的半径R=
,
则O到平面ACD1的距离d=
=
,
则圆锥的高h=
+
=
,
故圆锥的母线长l=
=
故圆锥的表面积为:πr(r+h)=
(
+
)π=
,
故答案为:
 解:如图,O为球心,也是正方体的中心,
解:如图,O为球心,也是正方体的中心,设球O被平面ACD1所截得的圆的半径为r,AC中点为M,
则r=
| 1 |
| 3 |
| ||
| 6 |
球的半径R=
| 1 |
| 2 |
则O到平面ACD1的距离d=
| R2-r2 |
| ||
| 6 |
则圆锥的高h=
| ||
| 6 |
| ||
| 2 |
2
| ||
| 3 |
故圆锥的母线长l=
| r2+h2 |
| ||
| 2 |
故圆锥的表面积为:πr(r+h)=
| ||
| 6 |
| ||
| 6 |
| ||
| 2 |
| 2π |
| 3 |
故答案为:
| 2π |
| 3 |
点评:本题考查了正方体和它的内接球的结构特征、圆锥的体积,关键是想象出截面图的形状,考查了空间想象能力.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
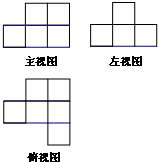 在一个仓库里堆积着正方体的货箱若干,要搬运这些箱子很困难,可是仓库管理员要清点一下箱子的数量,于是就想出一个办法:将这堆货物的三视图画了出来,你能根据三视图,帮他清点一下箱子的数量吗?这些正方体货箱的个数为( )
在一个仓库里堆积着正方体的货箱若干,要搬运这些箱子很困难,可是仓库管理员要清点一下箱子的数量,于是就想出一个办法:将这堆货物的三视图画了出来,你能根据三视图,帮他清点一下箱子的数量吗?这些正方体货箱的个数为( )| A、6 | B、7 | C、8 | D、9 |
某几何体三视图如下图所示,则该几何体的表面积为( )


| A、16-π | B、16+π |
| C、16-2π | D、16+2π |
若sinα=
,cos(α+β)=-
,且α,β是锐角,则β等于( )
4
| ||
| 7 |
| 11 |
| 14 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 (理科) 为了近似求出圆周率的值,有人设计如下方法来进行随机模拟:如图,双曲线
(理科) 为了近似求出圆周率的值,有人设计如下方法来进行随机模拟:如图,双曲线