题目内容
函数y=x2+2x的减区间是（ ）
| A、（-∞，-1] |
| B、[-1，+∞） |
| C、（-∞，0] |
| D、（-∞，+∞） |
考点：二次函数的性质
专题：函数的性质及应用
分析：本题可以通过二次函数的图象抛物线的对称轴方程得到函数的单调减区间，得到本题结论．
解答：
解：∵函数y=x2+2x，
∴函数图象为抛物线，开口向上，对称轴方程为：x=-1．
∴函数y=x2+2x的减区间是：（-∞，-1]．
故选A．
∴函数图象为抛物线，开口向上，对称轴方程为：x=-1．
∴函数y=x2+2x的减区间是：（-∞，-1]．
故选A．
点评：本题考查了二次的单调性，本题难度不大，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
若sinα=
，cos（α+β）=-
，且α，β是锐角，则β等于（ ）
4
| ||
| 7 |
| 11 |
| 14 |
A、
| ||
B、
| ||
C、
| ||
D、
|
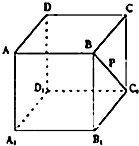如图，点P在正方体ABCD-A1B1C1D1的面对角线BC1上运动，则下列结论：①三棱锥A-D1PC的体积不变；②A1P∥平面ACD1；③DP⊥BC1；④平面PDB1⊥平面ACD1．其中正确的结论的个数是（ ）| A、1个 | B、2个 | C、3个 | D、4个 |
已知f（x）=
为偶函数，则y=loga（x2-4x-5）的单调递增区间为（ ）
|
| A、（-∞，-1） |
| B、（-∞，2） |
| C、（2，+∞） |
| D、（5，+∞） |