题目内容

3．已知a、b∈R，且2ab+2a2+2b2-9=0，若M为a2+b2的最小值，则约束条件$\left\{\begin{array}{l}0≤y≤\sqrt{{M^2}-{x^2}}\\ x-y≥-M\\ x+y≤M.\end{array}\right.$所确定的平面区域内整点（横坐标纵坐标均为整数的点）的个数为（　　）
A．9B．13C．16D．18

分析 根据基本不等式的性质求出M的值，利用数形结合进行求解即可．

解答 解：由2ab+2a2+2b2-9=0结合2ab≤a2+b2得3（a2+b2）≥9⇒a2+b2≥3（当且仅当a=b时等号成立）
故M=3，故约束条件确定的平面区域如右图阴影所示，在区域内，
在x轴上整点有7个，在直线x=1上有5个，在x=2上有3个，
在x=3上有1个，共16个．

故选：C

点评 本题主要考查线性规划的应用，利用基本不等式的性质求出M的值是解决本题的关键．综合性较强．

练习册系列答案
相关题目
13．已知向量$\overrightarrow{a}$=（2sinx，$\sqrt{3}$sinx），$\overrightarrow{b}$=（sinx，2cosx），函数f（x）=2$\overrightarrow{a}$•$\overrightarrow{b}$，若不等式f（x）≤m在[0，$\frac{π}{2}$]上有解，则实数m的最小值为（　　）
A．0B．-1C．2D．-2
14．已知平面向量$\overrightarrow{a}$=（1，0），$\overrightarrow{b}$=（-$\frac{1}{2}$，$\frac{\sqrt{3}}{2}$），则$\overrightarrow{a}$与$\overrightarrow{a}$+$\overrightarrow{b}$的夹角为（　　）
A．$\frac{π}{6}$B．$\frac{π}{3}$C．$\frac{2π}{3}$D．$\frac{5π}{6}$
11．一几何体的三视图如图示，则该几何体的体积为30．
18．已知直线l的参数方程为$\left\{{\begin{array}{l}{x=-1+tcosα}\\{y=1+tsinα}\end{array}}\right.$（t为参数）．以O为极点，x轴的非负半轴为极轴建立极坐标系，曲线C的极坐标方程为ρ=ρcosθ+2．
（Ⅰ）写出直线l经过的定点的直角坐标，并求曲线C的普通方程；
（Ⅱ）若$α=\frac{π}{4}$，求直线l的极坐标方程，以及直线l与曲线C的交点的极坐标．
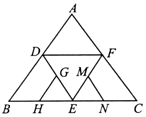8．如图是正四面体的平面展开图，G，H，M，N分别为DE，BE，EF，EC的中点，在这个正四面体中，有以下结论：
①GH与EF平行；
②BE与MN为异面直线；
③GH与AF成60°角；
④MN∥平面ADF；
其中正确结论的序号是③④．
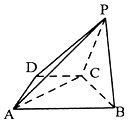15．如图，已知四棱锥P-ABCD中，底面ABCD是直角梯形，∠ADC=90°，AB∥CD，AD=DC=$\frac{1}{2}$AB=$\sqrt{2}$，平面PBC⊥平面ABCD．
（1）求证：AC⊥PB；
（2）在侧棱PA上是否存在一点M，使得DM∥平面PCB？若存在，试给出证明；若不存在，说明理由．
12．设函数f（x）=ln（1+ax）+bx，g（x）=f（x）-bx2．
（Ⅰ）若a=1，b=-1，求函数f（x）的单调区间；
（Ⅱ）若曲线y=g（x）在点（1，ln3）处的切线与直线11x-3y=0平行．
（i）  求a，b的值；
（ii）求实数k（k≤3）的取值范围，使得g（x）＞k（x2-x）对x∈（0，+∞）恒成立．
13．某次比赛甲得分的茎叶图如图所示，若去掉一个最高分，去掉一个最低分，则剩下4个分数的方差为14．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网