题目内容
14.已知平面向量$\overrightarrow{a}$=(1,0),$\overrightarrow{b}$=(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),则$\overrightarrow{a}$与$\overrightarrow{a}$+$\overrightarrow{b}$的夹角为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
分析 利用两个向量的数量积的定义,两个向量坐标形式的运算法则,求得cosθ=$\frac{\overrightarrow{a}•(\overrightarrow{a}+\overrightarrow{b})}{|\overrightarrow{a}|•|\overrightarrow{a}+\overrightarrow{b}|}$ 的值,可得θ的值.
解答 解:∵向量$\overrightarrow{a}$=(1,0),$\overrightarrow{b}$=(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),∴$\overrightarrow{a}$+$\overrightarrow{b}$=($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),$\overrightarrow{a}$•($\overrightarrow{a}$+$\overrightarrow{b}$)=(1,0)•($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$)=$\frac{1}{2}$,
设$\overrightarrow{a}$与$\overrightarrow{a}$+$\overrightarrow{b}$的夹角为θ,θ∈[0,π],则由cosθ=$\frac{\overrightarrow{a}•(\overrightarrow{a}+\overrightarrow{b})}{|\overrightarrow{a}|•|\overrightarrow{a}+\overrightarrow{b}|}$=$\frac{\frac{1}{2}}{1×1}$=$\frac{1}{2}$,可得θ=$\frac{π}{3}$,
故选:B.
点评 本题主要考查两个向量的数量积的定义,两个向量坐标形式的运算,属于基础题.

 某四棱锥的三视图如图所示,其俯视图为等腰直角三角形,则该四棱锥的体积为( )
某四棱锥的三视图如图所示,其俯视图为等腰直角三角形,则该四棱锥的体积为( )| A. | $\frac{{2\sqrt{2}}}{3}$ | B. | $\frac{4}{3}$ | C. | $\sqrt{2}$ | D. | 4 |
| A. |  | B. | 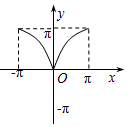 | C. | 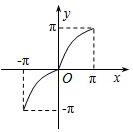 | D. | 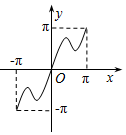 |