题目内容
15.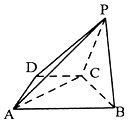 如图,已知四棱锥P-ABCD中,底面ABCD是直角梯形,∠ADC=90°,AB∥CD,AD=DC=$\frac{1}{2}$AB=$\sqrt{2}$,平面PBC⊥平面ABCD.
如图,已知四棱锥P-ABCD中,底面ABCD是直角梯形,∠ADC=90°,AB∥CD,AD=DC=$\frac{1}{2}$AB=$\sqrt{2}$,平面PBC⊥平面ABCD.(1)求证:AC⊥PB;
(2)在侧棱PA上是否存在一点M,使得DM∥平面PCB?若存在,试给出证明;若不存在,说明理由.
分析 (1)取AB的中点E,连结CE,推导出四边形AECD是正方形,从而CE⊥AB,由勾股定理得AC⊥CB,从而AC⊥平面PBC,由此能证明AC⊥PB.
(2)当M为侧棱PA的中点时,取PB的中点N,连接DM,MN,CN.推导出四边形MNCD为平行四边形,从而DM∥CN,由此能证明DM∥平面PCB.
解答 证明:(1)取AB的中点E,连结CE,
∵AB∥CD,$DC=\frac{1}{2}AB$,
∴DC∥AE,DC=AE,
∴四边形AECD是平行四边形.
又∵∠ADC=90°,∴四边形AECD是正方形,
∴CE⊥AB.
∴△CAB为等腰三角形,且$CA=CB=2,AB=2\sqrt{2}$,
∴AC2+CB2=AB2,∴AC⊥CB,…(3分)
∵平面PBC⊥平面ABCD,平面PBC∩平面ABCD=BC,AC⊥CB,
AC?平面ABCD.
∴AC⊥平面PBC.
又∵PB?平面PBC,∴AC⊥PB.…(6分)
解:(2)当M为侧棱PA的中点时,DM∥平面PCB.…(7分)
证明:取PB的中点N,连接DM,MN,CN.
在△PAB中,MN为中位线,∴MN∥AB,$MN=\frac{1}{2}AB=\sqrt{2}$.
由已知AB∥CD,所以MN∥CD.
又$MN=CD=\sqrt{2}$,∴四边形MNCD为平行四边形.∴DM∥CN.…(10分)
又DM?平面PCB,CN?平面PCB,∴DM∥平面PCB.…(12分)
点评 本题考查线线垂直的证明,考查满足线面平行的点的位置的确定与证明,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
6.函数y=x+sin|x|,x∈[-π,π]的大致图象是( )
| A. |  | B. | 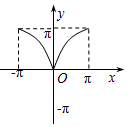 | C. | 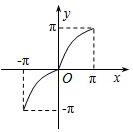 | D. | 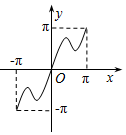 |
10.在平行四边形ABCD中,已知AB=2,AD=l,∠BAD=60°,若E,F分别是BC,CD的中点,则$\overrightarrow{BF}•\overrightarrow{DE}$=( )
| A. | 2 | B. | -2 | C. | $\frac{5}{4}$ | D. | $-\frac{5}{4}$ |
20.执行如图所示的程序框图,若输入的x值为1,则输出的k值为( )


| A. | 3 | B. | 4 | C. | 5 | D. | 6 |