题目内容
11．一几何体的三视图如图示，则该几何体的体积为30．
分析 首先根据三视图把平面图转换成立体图形，进一步利用几何体的体积公式求出结果．
解答 解：由题意，直观图是直四棱柱，底面为侧视图，高为5，体积V=$\frac{2+4}{2}×2×5$=30．
故答案为30．
点评 本题考查的知识要点：三视图和立体图之间的转换，几何体的体积公式的应用，主要考查学生的空间想象能力和应用能力．
练习册系列答案
阅读快车系列答案
相关题目
1．
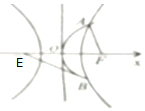已知E，F为双曲线$C：\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（0＜a＜b）$的左右焦点，抛物线y2=2px（p＞0）与双曲线有公共的焦点F，且与双曲线交于A、B不同两点，若5|AF|=4|EF|，则双曲线的离心率为（ ）
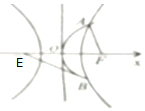已知E，F为双曲线$C：\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（0＜a＜b）$的左右焦点，抛物线y2=2px（p＞0）与双曲线有公共的焦点F，且与双曲线交于A、B不同两点，若5|AF|=4|EF|，则双曲线的离心率为（ ）| A． | $4+\sqrt{7}$ | B． | $4-\sqrt{3}$ | C． | $4+\sqrt{3}$ | D． | $4-\sqrt{7}$ |
2．
某四棱锥的三视图如图所示，其俯视图为等腰直角三角形，则该四棱锥的体积为（ ）
某四棱锥的三视图如图所示，其俯视图为等腰直角三角形，则该四棱锥的体积为（ ）| A． | $\frac{{2\sqrt{2}}}{3}$ | B． | $\frac{4}{3}$ | C． | $\sqrt{2}$ | D． | 4 |
6．函数y=x+sin|x|，x∈[-π，π]的大致图象是（ ）
| A． |  | B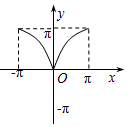． |  | C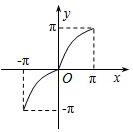． |  | D． |  |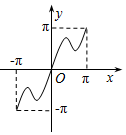
20．执行如图所示的程序框图，若输入的x值为1，则输出的k值为（ ）
| A． | 3 | B． | 4 | C． | 5 | D． | 6 |