题目内容
13.已知向量$\overrightarrow{a}$=(2sinx,$\sqrt{3}$sinx),$\overrightarrow{b}$=(sinx,2cosx),函数f(x)=2$\overrightarrow{a}$•$\overrightarrow{b}$,若不等式f(x)≤m在[0,$\frac{π}{2}$]上有解,则实数m的最小值为( )| A. | 0 | B. | -1 | C. | 2 | D. | -2 |
分析 利用两个向量的数量积的定义,三角恒等变换化简函数f(x)的解析式,再利用正弦函数的定义域和值域,求得f(x)的范围,可得m的最小值.
解答 解:∵函数f(x)=2$\overrightarrow{a}$•$\overrightarrow{b}$=4sin2x+4$\sqrt{3}$sinxcosx=2-2cos2x+2$\sqrt{3}$sin2x=4sin(2x-$\frac{π}{6}$)+2,
在[0,$\frac{π}{2}$]上,2x-$\frac{π}{6}$∈[-$\frac{π}{6}$,$\frac{5π}{6}$],∴4sin(2x-$\frac{π}{6}$)∈[-2,4],∴f(x)∈[0,6].
若不等式f(x)≤m在[0,$\frac{π}{2}$]上有解,则m≥0,
故选:A.
点评 本题主要考查两个向量的数量积的定义,三角恒等变换,正弦函数的定义域和值域,函数的能成立问题,属于中档题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
1.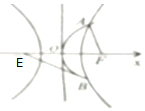 已知E,F为双曲线$C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(0<a<b)$的左右焦点,抛物线y2=2px(p>0)与双曲线有公共的焦点F,且与双曲线交于A、B不同两点,若5|AF|=4|EF|,则双曲线的离心率为( )
已知E,F为双曲线$C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(0<a<b)$的左右焦点,抛物线y2=2px(p>0)与双曲线有公共的焦点F,且与双曲线交于A、B不同两点,若5|AF|=4|EF|,则双曲线的离心率为( )
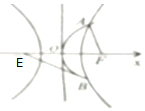 已知E,F为双曲线$C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(0<a<b)$的左右焦点,抛物线y2=2px(p>0)与双曲线有公共的焦点F,且与双曲线交于A、B不同两点,若5|AF|=4|EF|,则双曲线的离心率为( )
已知E,F为双曲线$C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(0<a<b)$的左右焦点,抛物线y2=2px(p>0)与双曲线有公共的焦点F,且与双曲线交于A、B不同两点,若5|AF|=4|EF|,则双曲线的离心率为( )| A. | $4+\sqrt{7}$ | B. | $4-\sqrt{3}$ | C. | $4+\sqrt{3}$ | D. | $4-\sqrt{7}$ |
8.在△ABC中,D是AC中点,延长AB至E,BE=AB,连接DE交BC于点F,则$\overrightarrow{AF}$=( )
| A. | $\frac{2}{5}$$\overrightarrow{AB}$+$\frac{3}{5}$$\overrightarrow{AC}$ | B. | $\frac{3}{5}$$\overrightarrow{AB}$+$\frac{2}{5}$$\overrightarrow{AC}$ | C. | $\frac{3}{4}$$\overrightarrow{AB}$+$\frac{1}{4}$$\overrightarrow{AC}$ | D. | $\frac{2}{3}$$\overrightarrow{AB}$+$\frac{1}{3}$$\overrightarrow{AC}$ |
2. 某四棱锥的三视图如图所示,其俯视图为等腰直角三角形,则该四棱锥的体积为( )
某四棱锥的三视图如图所示,其俯视图为等腰直角三角形,则该四棱锥的体积为( )
 某四棱锥的三视图如图所示,其俯视图为等腰直角三角形,则该四棱锥的体积为( )
某四棱锥的三视图如图所示,其俯视图为等腰直角三角形,则该四棱锥的体积为( )| A. | $\frac{{2\sqrt{2}}}{3}$ | B. | $\frac{4}{3}$ | C. | $\sqrt{2}$ | D. | 4 |