��Ŀ����
18����ֱ֪��l�IJ�������Ϊ$\left\{{\begin{array}{l}{x=-1+tcos��}\\{y=1+tsin��}\end{array}}\right.$��tΪ����������OΪ���㣬x��ķǸ�����Ϊ���Ὠ��������ϵ������C�ļ����귽��Ϊ��=��cos��+2������д��ֱ��l�����Ķ����ֱ�����꣬��������C����ͨ���̣�
������$��=\frac{��}{4}$����ֱ��l�ļ����귽�̣��Լ�ֱ��l������C�Ľ���ļ����꣮
���� �����ɲ������̿ɵö������꣬����x=��cos�ȣ�y=��sin�ȣ���2=x2+y2��ƽ�����ɵõ�������ͨ���̣�
����д��ֱ��l�IJ������̺���ͨ���̣����ֱ������ͼ�����Ĺ�ϵ���ɵ�ֱ�ߵļ����귽�̣�����������C�ļ����귽�̣����ɵõ�����ļ����꣮
��� �⣺����ֱ��l�������㣨-1��1����-----------------------------------------------------------------��2�֣�
�ɦ�=��cos��+2�æ�2=����cos��+2��2��
������C����ͨ����Ϊx2+y2=��x+2��2�������y2=4x+4��---��5�֣�
������$��=\frac{��}{4}$����$\left\{{\begin{array}{l}{x=-1+\frac{{\sqrt{2}}}{2}t}\\{y=1+\frac{{\sqrt{2}}}{2}t}\end{array}}\right.$����ͨ����Ϊy=x+2��----------------------------------��6�֣�
��ֱ��l�ļ����귽��Ϊ��sin��=��cos��+2��------------------------------------------------��8�֣�
��������C����=��cos��+2��
��sin��=1��ȡ$��=\frac{��}{2}$���æ�=2������ֱ��l������C�Ľ���Ϊ$��2��\;\frac{��}{2}��$��------------��10�֣�
���� ���⿼�鼫���귽�̺���ͨ���̵Ļ��������黯���������������������ڻ����⣮

| A�� | $\frac{2}{5}$$\overrightarrow{AB}$+$\frac{3}{5}$$\overrightarrow{AC}$ | B�� | $\frac{3}{5}$$\overrightarrow{AB}$+$\frac{2}{5}$$\overrightarrow{AC}$ | C�� | $\frac{3}{4}$$\overrightarrow{AB}$+$\frac{1}{4}$$\overrightarrow{AC}$ | D�� | $\frac{2}{3}$$\overrightarrow{AB}$+$\frac{1}{3}$$\overrightarrow{AC}$ |
| A�� |  | B�� | 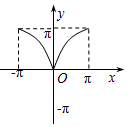 | C�� | 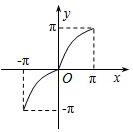 | D�� | 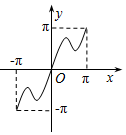 |
| A�� | 2 | B�� | -2 | C�� | $\frac{5}{4}$ | D�� | $-\frac{5}{4}$ |